Introdução
Trabalho com planejamento da Construção Civil e é comum utilizarmos muito o conceito de transformar Cronogramas de Obra em Curvas S do sistema cartesiano. Dividimos o eixo X em períodos iguais da Obra, como por exemplo os meses de sua duração, No Y inserimos as %s acumuladas de cada ponto. Fazemos o acompanhamento do cronograma por atividade e vamos lançando nas datas específicas as %s reais relativas ao cumprimento de cada tarefa, o somatório nos dá uma % total realizada que comparamos com a prevista. Através desta fica fácil visualizar graficamente o acompanhamento do previsto x realizado ( 2 curvas) e medir atrasos de obra. Portanto minha dúvida tem a ver com Curvas S. O Objetivo final é manipular a equação da Curva S através de duas incógnitas de forma que graficamente podemos nos aproximar de uma curva S perfeita. A hipótese é a de que um cronograma inicial de obra (previsto) bem equilibrado tem o formato de um S graficamente bem arredondado e sem subidas bruscas.
Construção do Enunciado
Criei no sistema de coordenadas cartesiano ( através do programa excell) 2 curvas em formato de S, cada uma com fórmulas diferentes e agora estou tentando igualá-las. Cada uma destas curvas tem como pares ordenados 22 períodos em X e 22 %s acumuladas em Y.
A primeira é a Curva S é a perfeita representada aqui pela função sigmoidal. A sigmoidal só funciona bem entre os valores -6 e 6.Portanto dividi 6/13 = 0,4615 (com 13 casas depois da virgula) e fui do 4,615 ao - 5,0769 passando pelo 0 para os valores de x. Fórmula: 1/1
 . Os pontos desta função são pt1(4,615;0,98%),pt2(4,1513;1,55%) .... pt 11(0;50%) ... pt 22(-5,07692;99,38%)
. Os pontos desta função são pt1(4,615;0,98%),pt2(4,1513;1,55%) .... pt 11(0;50%) ... pt 22(-5,07692;99,38%)A segunda curva é a teórica que virá de um cronograma real. Esta tem duas incógnitas e é uma função que se usa no ramo para a construção da curva S.
![y=1-[{1-{(\frac{n}{N}})^{logI}]^{s} y=1-[{1-{(\frac{n}{N}})^{logI}]^{s}](/latexrender/pictures/14e0a5eed5ee86e18788a703c5e41b3d.png)
Onde y é % acumulada , n é o valor do período (no caso um número de 1 a 22), N é o número total de períodos (22), I é um coeficiente que dá forma a curva S ( acredito que seja no primeiro trecho?) e S idem (com relação a segunda curvatura???).
Depois de muitas tentativas gráficas inseri os valores de I = 700 log I = 2,8450 e s = 5. As duas curvas estão próximas mas não estão iguais.
Os pontos foram pt1 (1;0,08%), pt2(2;0,54%) ...pt 11(11;52,73%) ....pt 20 ( 20;99,92%)pt 21(21,100%) pt 22(22,100%)
Dúvida - Igualando duas equações
Uma equação tem uma incógnita. A outra tem duas. Utilizando o ponto 11 em ambas as equações cheguei em
 . E não saio disso. E também não tenho absoluta certeza se meu desenvolvimento está correto.
. E não saio disso. E também não tenho absoluta certeza se meu desenvolvimento está correto.Estou tentando fixar o s em um valor fixo, como por exemplo 5 e tentar descobri um I e logI válido que iguale as % em todos os 22 pontos.Um a curva ficaria portanto igual a outra e aprenderia a manipular graficamente a Curva S.
Posso de bom grado fornecer o arquivo excell. Acredito será mais fácil.
Espero ter sido claro.
Muito Obrigado.
João Petrocelle -
jpetrocelle@gmail.com




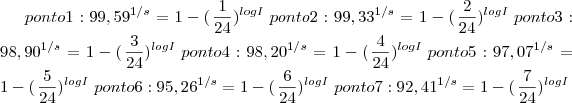
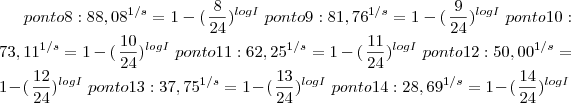
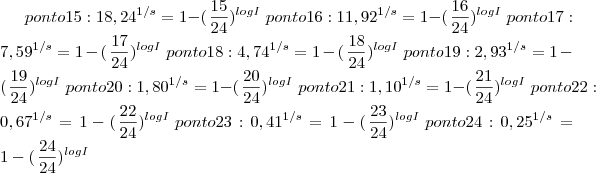


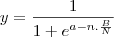
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)