 por Joao Petrocelle » Sex Set 14, 2012 09:13
por Joao Petrocelle » Sex Set 14, 2012 09:13
Agradeço pela oportunidade.
IntroduçãoTrabalho com planejamento da Construção Civil e é comum utilizarmos muito o conceito de transformar Cronogramas de Obra em Curvas S do sistema cartesiano. Dividimos o eixo X em períodos iguais da Obra, como por exemplo os meses de sua duração, No Y inserimos as %s acumuladas de cada ponto. Fazemos o acompanhamento do cronograma por atividade e vamos lançando nas datas específicas as %s reais relativas ao cumprimento de cada tarefa, o somatório nos dá uma % total realizada que comparamos com a prevista. Através desta fica fácil visualizar graficamente o acompanhamento do previsto x realizado ( 2 curvas) e medir atrasos de obra. Portanto minha dúvida tem a ver com Curvas S. O Objetivo final é manipular a equação da Curva S através de duas incógnitas de forma que graficamente podemos nos aproximar de uma curva S perfeita. A hipótese é a de que um cronograma inicial de obra (previsto) bem equilibrado tem o formato de um S graficamente bem arredondado e sem subidas bruscas.
Construção do EnunciadoCriei no sistema de coordenadas cartesiano ( através do programa excell) 2 curvas em formato de S, cada uma com fórmulas diferentes e agora estou tentando igualá-las. Cada uma destas curvas tem como pares ordenados 22 períodos em X e 22 %s acumuladas em Y.
A primeira é a Curva S é a perfeita representada aqui pela função sigmoidal. A sigmoidal só funciona bem entre os valores -6 e 6.Portanto dividi 6/13 = 0,4615 (com 13 casas depois da virgula) e fui do 4,615 ao - 5,0769 passando pelo 0 para os valores de x. Fórmula: 1/1

. Os pontos desta função são pt1(4,615;0,98%),pt2(4,1513;1,55%) .... pt 11(0;50%) ... pt 22(-5,07692;99,38%)
A segunda curva é a teórica que virá de um cronograma real. Esta tem duas incógnitas e é uma função que se usa no ramo para a construção da curva S.
![y=1-[{1-{(\frac{n}{N}})^{logI}]^{s} y=1-[{1-{(\frac{n}{N}})^{logI}]^{s}](/latexrender/pictures/14e0a5eed5ee86e18788a703c5e41b3d.png)
Onde y é % acumulada , n é o valor do período (no caso um número de 1 a 22), N é o número total de períodos (22), I é um coeficiente que dá forma a curva S ( acredito que seja no primeiro trecho?) e S idem (com relação a segunda curvatura???).
Depois de muitas tentativas gráficas inseri os valores de I = 700 log I = 2,8450 e s = 5. As duas curvas estão próximas mas não estão iguais.
Os pontos foram pt1 (1;0,08%), pt2(2;0,54%) ...pt 11(11;52,73%) ....pt 20 ( 20;99,92%)pt 21(21,100%) pt 22(22,100%)
Dúvida - Igualando duas equaçõesUma equação tem uma incógnita. A outra tem duas. Utilizando o ponto 11 em ambas as equações cheguei em

. E não saio disso. E também não tenho absoluta certeza se meu desenvolvimento está correto.
Estou tentando fixar o s em um valor fixo, como por exemplo 5 e tentar descobri um I e logI válido que iguale as % em todos os 22 pontos.Um a curva ficaria portanto igual a outra e aprenderia a manipular graficamente a Curva S.
Posso de bom grado fornecer o arquivo excell. Acredito será mais fácil.
Espero ter sido claro.
Muito Obrigado.
João Petrocelle -
jpetrocelle@gmail.com
-
Joao Petrocelle
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Set 14, 2012 07:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Arquitetura / Administração
- Andamento: formado
 por young_jedi » Qua Out 03, 2012 11:24
por young_jedi » Qua Out 03, 2012 11:24
fala João Petrocelle, dei uma olhada como voce me falou aqui no seu poste
fiz algumas simulações e achei os seguintes valores
s=5,974

com esses valores cheguei nesse grafico feito no excel

- simulacao
a linha em vermelho é a sigmoide perfeita
e azul é a equação exponencial que voce postou com este valores para s e logI que eu coloquei
esse foi o maximo que consegui aproximar as duas curvas, não sei se é bem isso que voce queria mais ta ai.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Joao Petrocelle » Qua Out 03, 2012 12:51
por Joao Petrocelle » Qua Out 03, 2012 12:51
Muito obrigado young jedi. E isso mesmo que queria. Mas na verdade queria igualar . algo que parece nao ser possivel.
Eu vou postar um novo excell com novos valores, pois na epoca que fiz o post percebi um errinho . Vc poderia gerar novamente outros valores para duas incognitas?
Depois vc poderia me mostrar o desenvolvimento?
-
Joao Petrocelle
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Set 14, 2012 07:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Arquitetura / Administração
- Andamento: formado
 por young_jedi » Qua Out 03, 2012 13:00
por young_jedi » Qua Out 03, 2012 13:00
igualar ela em todos os pontos realmente é impossivel, mais da pra aproxima-las bastante, a melhor aproximação que eu encontrei foi essa
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Joao Petrocelle » Qua Out 03, 2012 17:20
por Joao Petrocelle » Qua Out 03, 2012 17:20
Jedi por favor veja o jpeg com os valores
para tentar igualar ainda mais vou te dar 24 pontos.
equações abaixo. por gentileza me informe s e log I e se possível me fale qual foi o desenvolvimento. irei mandar tb o grafico
[Unparseable or potentially dangerous latex formula. Error 1 ]
- Anexos
-

-
Joao Petrocelle
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Set 14, 2012 07:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Arquitetura / Administração
- Andamento: formado
 por Joao Petrocelle » Qua Out 03, 2012 17:32
por Joao Petrocelle » Qua Out 03, 2012 17:32
equacoes
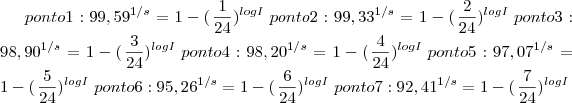
-
Joao Petrocelle
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Set 14, 2012 07:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Arquitetura / Administração
- Andamento: formado
 por Joao Petrocelle » Qua Out 03, 2012 17:37
por Joao Petrocelle » Qua Out 03, 2012 17:37
[Unparseable or potentially dangerous latex formula. Error 1 ]
-
Joao Petrocelle
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Set 14, 2012 07:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Arquitetura / Administração
- Andamento: formado
 por Joao Petrocelle » Qua Out 03, 2012 17:39
por Joao Petrocelle » Qua Out 03, 2012 17:39
-
Joao Petrocelle
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Set 14, 2012 07:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Arquitetura / Administração
- Andamento: formado
 por Joao Petrocelle » Qua Out 03, 2012 17:39
por Joao Petrocelle » Qua Out 03, 2012 17:39
-
Joao Petrocelle
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Set 14, 2012 07:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Arquitetura / Administração
- Andamento: formado
 por Joao Petrocelle » Qua Out 03, 2012 17:41
por Joao Petrocelle » Qua Out 03, 2012 17:41
grafico para jedi
- Anexos
-

- grafico
-
Joao Petrocelle
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Set 14, 2012 07:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Arquitetura / Administração
- Andamento: formado
 por young_jedi » Qua Out 03, 2012 17:58
por young_jedi » Qua Out 03, 2012 17:58
Então joao petrocelle com os novos valores que voce me passou eu encontrei


dai consegui o seguinte grafico

- simulacao
foi os melhores valores que consegui
os metodos que eu utilizei para chegar nesses valores nao foram os convencionais
eu utilizei um programa chamado matlab e ai fui simulando para diversos valores de s e logI tentando ter o menor erro possivel
ai cheguei nesses valores
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Joao Petrocelle » Qua Out 03, 2012 18:26
por Joao Petrocelle » Qua Out 03, 2012 18:26
Obrigado Jedi, tá otimo... a diferença entre os pontos varia pouco a maioria é menor que 2 %
jajá vou parar de encher o saco...rss
mas mais uma perguntinha...
veja a tabela com os valores de S e logI. A diferença é maior na trecho final e menor no começo. A coisa toda não dá certo porque a formula da curva S não consegue formar uma curva perfeita ( quero com isso dizer que ela não forma o trecho inferior igual ao trecho superior , considerando o ponto 12 como centro). Acho que tem a ver com elevar a Log I e depois elevar de novo a S que gera esse "erro". Vc saberia alterar a formula mantendo duas incognitas ( sei lá mudando a posição do S) para que ela pudesse vir a gerar uma curva perfeita?
Resumindo precisaria de uma formula que utiza duas incognitas e gera um s perfeito. Como a da sigmoide mas a sigmoide só tem uma incognita.
Agora vai um chute se base: Acho que seria um polinomio do segundo grau talvez... do tipo y = ax2 + bx + c
ponto 1 2 3 4 5 6 7 8 9 10 11
sigm 0,41% 0,67% 1,10% 1,80% 2,93% 4,74% 7,59% 11,92% 18,24% 26,89% 37,75%
sigm 0,00% 0,06% 0,29% 0,89% 2,12% 4,27% 7,66% 12,59% 19,26% 27,71% 37,76%
dif 0,40% 0,61% 0,81% 0,91% 0,81% 0,47% -0,08% -0,67% -1,02% -0,82% -0,01%
12 13 14 15 16 17 18 19 20 21 22 23
50,00% 62,25% 73,11% 81,76% 88,08% 92,41% 95,26% 97,07% 98,20% 98,90% 99,33% 99,59%
48,96% 60,59% 71,76% 81,56% 89,29% 94,65% 97,81% 99,32% 99,86% 99,98% 100,00% 100,00%
1,04% 1,66% 1,35% 0,20% -1,21% -2,24% -2,55% -2,25% -1,66% -1,08% -0,67% -0,41%
-
Joao Petrocelle
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Set 14, 2012 07:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Arquitetura / Administração
- Andamento: formado
 por young_jedi » Qua Out 03, 2012 21:13
por young_jedi » Qua Out 03, 2012 21:13
Joao petrocelle, desculpa não ter respondido antes é que eu tava meio atarefado.
Então da para aproximar de uma curva do segundo grau só que não fica uma aproximação muito boa
e tambem a equação tem tres parametros
a b e c
voce esta querendo uma equação com dois parametros eu sugeria a propria sigmoide
fazendo uma alteração
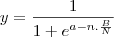
onde nesse caso a=6, B=12 e N=24
eu não sei se sua equação tem que seguir alguma regra ou se ela é baseada em alguma formula
se não for da pra usar isso ai.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função da curva S] Qual é Função desta curva?
por Joao Petrocelle » Qua Nov 14, 2012 14:45
- 7 Respostas
- 4405 Exibições
- Última mensagem por young_jedi

Qua Nov 14, 2012 21:19
Funções
-
- Comprimento de curva
por dsbonafe » Ter Out 13, 2009 16:39
- 1 Respostas
- 2752 Exibições
- Última mensagem por Camolas

Sex Mai 31, 2013 15:27
Cálculo: Limites, Derivadas e Integrais
-
- Curva borboleta
 por LuizAquino » Sáb Jul 30, 2011 13:51
por LuizAquino » Sáb Jul 30, 2011 13:51
- 1 Respostas
- 2111 Exibições
- Última mensagem por Neperiano

Sáb Ago 20, 2011 22:39
Assuntos Gerais ou OFF-TOPIC
-
- Comprimento da curva
por Crist » Qui Nov 29, 2012 13:32
- 6 Respostas
- 3696 Exibições
- Última mensagem por young_jedi

Ter Dez 11, 2012 11:01
Cálculo: Limites, Derivadas e Integrais
-
- Comprimento de Curva
por Marcossiva » Sex Jun 28, 2013 10:59
- 3 Respostas
- 2180 Exibições
- Última mensagem por Marcossiva

Sex Jun 28, 2013 11:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Os pontos desta função são pt1(4,615;0,98%),pt2(4,1513;1,55%) .... pt 11(0;50%) ... pt 22(-5,07692;99,38%)
. Os pontos desta função são pt1(4,615;0,98%),pt2(4,1513;1,55%) .... pt 11(0;50%) ... pt 22(-5,07692;99,38%)![y=1-[{1-{(\frac{n}{N}})^{logI}]^{s} y=1-[{1-{(\frac{n}{N}})^{logI}]^{s}](/latexrender/pictures/14e0a5eed5ee86e18788a703c5e41b3d.png)
 . E não saio disso. E também não tenho absoluta certeza se meu desenvolvimento está correto.
. E não saio disso. E também não tenho absoluta certeza se meu desenvolvimento está correto.



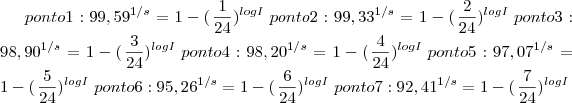
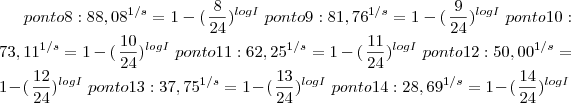
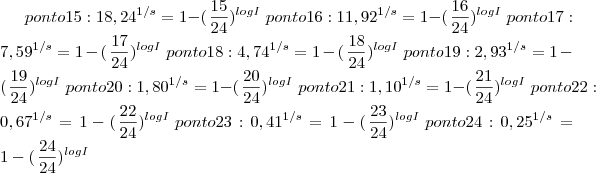


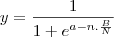
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: