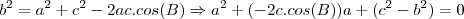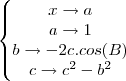por TOPO_PAIM » Sex Ago 17, 2012 01:45
por TOPO_PAIM » Sex Ago 17, 2012 01:45
Dado um triângulo qualquer, com suas dimensões: b=529,42; c=946,72 e ângulo B=33º03'56". Calcular os restantes dos ângulos internos (A e C) e o valor do lado a.
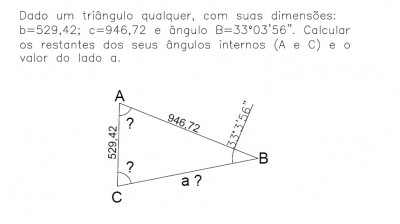
- Questão a ser resolvida
Tentei aplicar a lei dos senos:
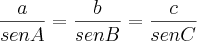
e a lei dos cossenos:
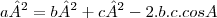
para descobrir a distancia do lado a.
Ja que possuo 2 lados e 1 ângulo, a formula cabível seria a
lei dos cossenos que ficaria assim: b²=a²+c²-2.a.c.cosB
529,42²=a²+946,72²-2.a.946,72.cos33º03'56"
Mas não foi possível o calculo.
E para calculo de ângulos é aplicável a formula:
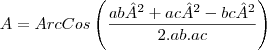
Acredito que o enunciado da questão informe algum dos elementos errado.
Vejo que para esse calculo ser possível eu deveria saber 2 lados do triangulo e o angulo que é dado pela vértice formada por esses dois lados, nessa questão seria o angulo A,mostrado na figura, e não o B, que é o existente.
Espero ajuda, muito obrigado.
-
TOPO_PAIM
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Ago 16, 2012 23:02
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informatica
- Andamento: formado
 por Russman » Sex Ago 17, 2012 01:59
por Russman » Sex Ago 17, 2012 01:59
O seu problema é determinar a terceira medida de um triângulo sabendo apenas duas medidas e um ângulo interno.
Suponhamos que os lados

e

do triângulo sejam conhecidos, bem como o angulo interno

oposto ao lado de medida

. Assim, do Teorema dos Cossenos, temos
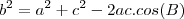
Como os valores

,

e
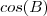
são conhecido você fica com uma equação de 2° grau em

bem simples de resolver!
Quanto aos outros ângulos: Lembre-se que
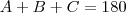
. Assim, como

é conhecido basta determinarmos ou

ou

que o restante fica explicito!
Optarei por deteminar

. Uma maneira é usar novamente o TeoremaDosCossenos:
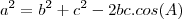
de onde você pode facilmente isolar

uma vez que

e

são conhecidos!.
Calculado o valor de

, basta tomar
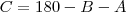
e seu problema esta solucionado!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por TOPO_PAIM » Sex Ago 17, 2012 12:34
por TOPO_PAIM » Sex Ago 17, 2012 12:34
Russman escreveu:O seu problema é determinar a terceira medida de um triângulo sabendo apenas duas medidas e um ângulo interno.
Suponhamos que os lados

e

do triângulo sejam conhecidos, bem como o angulo interno

oposto ao lado de medida

. Assim, do Teorema dos Cossenos, temos
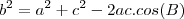
Como os valores

,

e
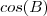
são conhecido você fica com uma equação de 2° grau em

bem simples de resolver!
Quanto aos outros ângulos: Lembre-se que
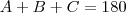
. Assim, como

é conhecido basta determinarmos ou

ou

que o restante fica explicito!
Optarei por deteminar

. Uma maneira é usar novamente o TeoremaDosCossenos:
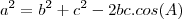
de onde você pode facilmente isolar

uma vez que

e

são conhecidos!.
Calculado o valor de

, basta tomar
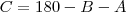
e seu problema esta solucionado!
Caro amigo Russman, obrigado pela ajuda. Mas mesmo assim estou com dificuldade no desenvolvimento e na aplicação do teorema dos cossenos para descobrir o valor do lado "a"!
Seria possível você mostrar desenvolvimento para mim? Enquanto aos a resultados dos ângulos esta tranquilo.
Muito Obrigado
-
TOPO_PAIM
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Ago 16, 2012 23:02
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informatica
- Andamento: formado
 por Russman » Sex Ago 17, 2012 16:12
por Russman » Sex Ago 17, 2012 16:12
Sim.
Uma equação de 2° grau geral é da forma
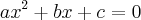
e, como você bem deve saber, a solução se apresenta como
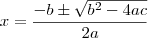
.
Observe que reescrevendo a equação de forma que
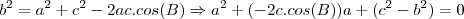
temos , comparando com a forma geral da equação de 2° grau,
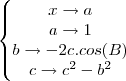
Ajudou?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- LEI DOS SENOS E COSSENOS
por MERLAYNE » Qua Abr 25, 2012 20:36
- 1 Respostas
- 1820 Exibições
- Última mensagem por Russman

Qua Abr 25, 2012 21:26
Trigonometria
-
- Teorema dos senos
por Maria Livia » Qua Out 03, 2012 10:25
- 2 Respostas
- 2341 Exibições
- Última mensagem por Maria Livia

Qua Out 03, 2012 15:54
Geometria Plana
-
- Valor numerico senos
por estudandoMat » Seg Abr 05, 2010 17:28
- 2 Respostas
- 1826 Exibições
- Última mensagem por estudandoMat

Seg Abr 05, 2010 21:21
Trigonometria
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6601 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- aplicaçao de EDO
por nayana_ac » Dom Set 19, 2010 01:28
- 3 Respostas
- 15279 Exibições
- Última mensagem por Krilitolxc

Ter Fev 02, 2016 07:40
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
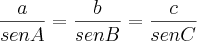 e a lei dos cossenos:
e a lei dos cossenos: 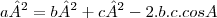 para descobrir a distancia do lado a.
para descobrir a distancia do lado a.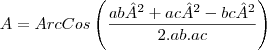


 e
e  do triângulo sejam conhecidos, bem como o angulo interno
do triângulo sejam conhecidos, bem como o angulo interno  oposto ao lado de medida
oposto ao lado de medida 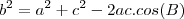
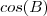 são conhecido você fica com uma equação de 2° grau em
são conhecido você fica com uma equação de 2° grau em  bem simples de resolver!
bem simples de resolver!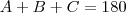 . Assim, como
. Assim, como  ou
ou  que o restante fica explicito!
que o restante fica explicito!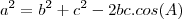
 e
e 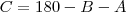 e seu problema esta solucionado!
e seu problema esta solucionado!
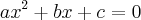 e, como você bem deve saber, a solução se apresenta como
e, como você bem deve saber, a solução se apresenta como 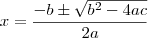 .
.