 por GuilhermeOliveira » Dom Jun 24, 2012 23:12
por GuilhermeOliveira » Dom Jun 24, 2012 23:12
Tenho aqui um exercício bem simples, porém, não sei como resolvê-lo.
Encontre uma base ortonormal B para o subespaço W de
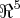
gerado pelos vetores:
v1=(1,1,1,0,1)
v2=(1,0,0,-1,1)
v3=(3,1,1,-2,3)
v4=(0,2,1,1-1)
Qual é a dimensão de W ?
Qual é a diferença entre uma base e um subespaço ?
OBS:
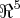
=((conjunto dos números reais)^5)
Tenho vários exercícios desse pra resolver e eu preciso de ajuda com este para poder entender o que deve ser feito e poder resolver o restante.
Muito obrigado.
Editado pela última vez por
GuilhermeOliveira em Seg Jun 25, 2012 11:55, em um total de 1 vez.
-
GuilhermeOliveira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Jun 24, 2012 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciência da computação
- Andamento: cursando
 por MarceloFantini » Seg Jun 25, 2012 01:24
por MarceloFantini » Seg Jun 25, 2012 01:24
Você já aprendeu o algoritmo de Gram-Schmidt? Esta é a solução para este problema.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por GuilhermeOliveira » Seg Jun 25, 2012 12:05
por GuilhermeOliveira » Seg Jun 25, 2012 12:05
Eu sei que a fórmula de Gram-Schmidt é

Mas e então ? Eu gostaria de saber como fica o desenvolvimento.
Valeu.
Editado pela última vez por
GuilhermeOliveira em Seg Jun 25, 2012 13:09, em um total de 1 vez.
-
GuilhermeOliveira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Jun 24, 2012 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciência da computação
- Andamento: cursando
 por GuilhermeOliveira » Seg Jun 25, 2012 13:08
por GuilhermeOliveira » Seg Jun 25, 2012 13:08
Acho que consegui compreender. Basta aplicar o processo de ortogonalização de Gram-Schmidit para obter vetores ortogonais que formam o mesmo subespaço deste.
Muito obrigado.
-
GuilhermeOliveira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Jun 24, 2012 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciência da computação
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dimensoes e bases em R3
por ThunderHawk » Dom Mar 15, 2009 08:09
- 0 Respostas
- 1865 Exibições
- Última mensagem por ThunderHawk

Dom Mar 15, 2009 08:09
Álgebra Elementar
-
- EXERCICIO PROPOSTO-dimensoes de um observatorio..
por adauto martins » Qua Out 01, 2014 12:23
- 0 Respostas
- 1893 Exibições
- Última mensagem por adauto martins

Qua Out 01, 2014 12:23
Cálculo: Limites, Derivadas e Integrais
-
- [Bases Ortonormais] - Ajuda Exercício
por Anna_lu » Seg Mar 23, 2015 14:23
- 1 Respostas
- 1014 Exibições
- Última mensagem por adauto martins

Seg Mar 23, 2015 19:33
Geometria Analítica
-
- Traçado rápido de curva clássica
por Daniel SSousa » Dom Nov 18, 2012 21:48
- 4 Respostas
- 2949 Exibições
- Última mensagem por Daniel SSousa

Ter Nov 20, 2012 00:30
Geometria Analítica
-
- URGENTE! TEOREMA DE THALES RAPIDO POR FAVOR
por Joony » Ter Jul 21, 2009 21:27
- 3 Respostas
- 2454 Exibições
- Última mensagem por Joony

Qua Jul 22, 2009 22:30
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
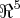 gerado pelos vetores:
gerado pelos vetores: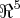 =((conjunto dos números reais)^5)
=((conjunto dos números reais)^5)



