


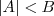 , teremos que
, teremos que 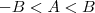 (valendo isso caso seja
(valendo isso caso seja  ), contando que
), contando que  e
e  são números reais.
são números reais. ou
ou  a relação seria outra. Qual?
a relação seria outra. Qual? , então
, então 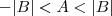 e daí você terá que estudar cada caso separado, ou seja,
e daí você terá que estudar cada caso separado, ou seja, 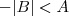 e
e 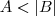 e, por fim, fazer as devidas interseções dos conjuntos que satisfazem as relações.
e, por fim, fazer as devidas interseções dos conjuntos que satisfazem as relações.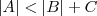 (
( um número real), onde deverá ser feito
um número real), onde deverá ser feito 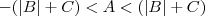 .
.

pipinha1982 escreveu:entao mas nao tenho de elevar cada modulo ao quadrado? :( nao pesco nada disto se me poder ajudar








 é o conjunto dos números reais
é o conjunto dos números reais



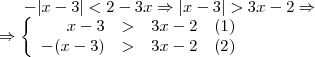
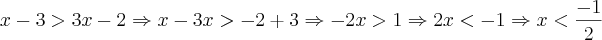

 se
se 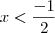 ou
ou  , ou seja, se
, ou seja, se  .
. :
: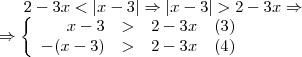
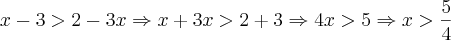

 se
se 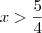 ou
ou 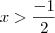 , ou seja, se
, ou seja, se 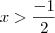 .
. se
se  e
e 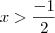 , ou seja, se
, ou seja, se  .
.

 possui raízes em
possui raízes em  e em
e em 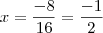 (encontradas utilizando a fórmula de Bhaskara).
(encontradas utilizando a fórmula de Bhaskara).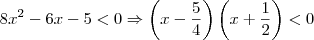 .
.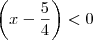 (1) e
(1) e  (2)
(2) (3) e
(3) e  (4).
(4).
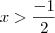

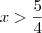
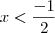
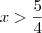 e
e 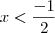 , a inequação
, a inequação  será falsa.
será falsa. ...
...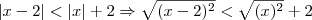

 se
se  .
.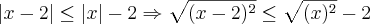

 real.
real.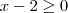 sempre, ou seja,
sempre, ou seja, 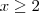 .
.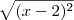 não pode ser negativo. Assim sendo
não pode ser negativo. Assim sendo 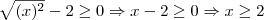

pipinha1982 escreveu:boa tarde ant_dii
sera que me podia ajudar na resolucao das inequacoes
?
obrigado

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

