eu tenho esse grafico abaixo:
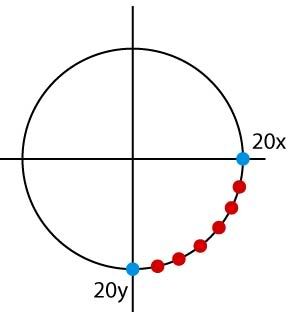
os pontos azuis são (20,0) o da direita e (0,20) o de baixo (o programa que vou usar interpreta como negativo acima do grafico e positivo pra baixo). O que eu preciso é descobrir as coordenadas no grafico dos pontos vermelhos, sendo que eles tem a mesma distancia entre eles e são 6 pontos
a variacao de inclinacao do angulo de um pra outro é 12.85714 eu apenas dividí 90/7, creio que isso seja muito facil mas nao sei a formula que uso pra resolver, eu gostaria de saber a formula pra resolver esse probleminha e descobrir essas coordenadas
abraços
são conhecidos e há triângulos retângulos com as projeções:
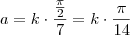
variar em seu projeto, com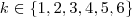 
.
da circunferência de raio 
e centro 
, tal que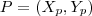 
, então temos: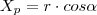
o ângulo formado por 
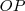e o eixo x.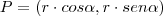
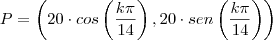
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.