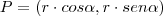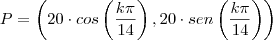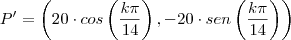por cristfc » Qua Nov 05, 2008 15:43
por cristfc » Qua Nov 05, 2008 15:43
minha pergunta é simples, na verdade não é pra nenhum curso nem nada, é pra um projeto pessoal mesmo..
eu tenho esse grafico abaixo:
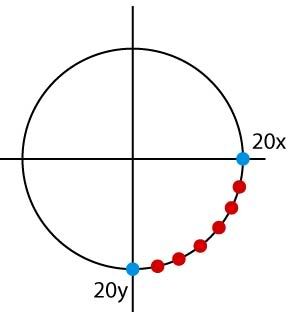
os pontos azuis são (20,0) o da direita e (0,20) o de baixo (o programa que vou usar interpreta como negativo acima do grafico e positivo pra baixo). O que eu preciso é descobrir as coordenadas no grafico dos pontos vermelhos, sendo que eles tem a mesma distancia entre eles e são 6 pontos
a variacao de inclinacao do angulo de um pra outro é 12.85714 eu apenas dividí 90/7, creio que isso seja muito facil mas nao sei a formula que uso pra resolver, eu gostaria de saber a formula pra resolver esse probleminha e descobrir essas coordenadas

abraços
-
cristfc
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 04, 2008 15:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por admin » Qua Nov 05, 2008 19:18
por admin » Qua Nov 05, 2008 19:18
Olá
cristfc, boas-vindas!
Sobre o programa interpretando o eixo y invertido, não se preocupe para o cálculo. Após obter as coordenadas procuradas, multiplique a ordenada y por -1 para refletir o ponto com relação ao eixo x.
Veja se esta figura ajuda:
Como você pode ver, podemos utilizar as funções seno e cosseno, já que os ângulos

são conhecidos e há triângulos retângulos com as projeções:
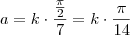
Faça

variar em seu projeto, com
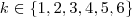
.
Note que representei o ângulo em radianos.
Cuidado ao utilizar as funções seno e cosseno em seu projeto pois normalmente os argumentos são esperados em radianos, não em graus.
Em resumo, dado um ponto

da circunferência de raio

e centro

, tal que
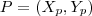
, então temos:
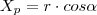

Sendo

o ângulo formado por
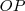
e o eixo x.
Variando o ângulo, as coordenadas serão:
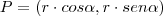
Para o caso particular:
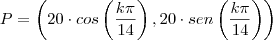
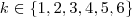
Antes de utilizar, você precisa considerar a reflexão do ponto:
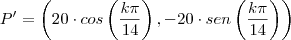
Espero ter ajudado!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por cristfc » Seg Nov 10, 2008 22:04
por cristfc » Seg Nov 10, 2008 22:04
obrigado, ajudou sim, e muito, finalmente conseguiu resolver isso.. estava quebrando a cabeça. vou por seu nome dos creditos hehehe :P
um abraço
-
cristfc
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 04, 2008 15:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por edwinaclima » Sáb Jul 10, 2010 11:44
por edwinaclima » Sáb Jul 10, 2010 11:44
Bom dia!
Preciso calcular o raio a partir de 3 coordenadas cartesianas. Como faço?
x y
8,59,-15,85
-3,87,-9,58
-12,35,-15,21
Dese já agradeço a ajuda
Edwin
-
edwinaclima
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Jul 10, 2010 11:35
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ângulos numa Circunferência] (UNIFOR-CE/1998)
 por eiji » Sex Abr 13, 2012 20:57
por eiji » Sex Abr 13, 2012 20:57
- 2 Respostas
- 9911 Exibições
- Última mensagem por eiji

Sex Abr 13, 2012 21:28
Geometria Plana
-
- Circunferência inscrita numa secção circular
 por Guga1981 » Ter Out 17, 2017 19:14
por Guga1981 » Ter Out 17, 2017 19:14
- 1 Respostas
- 3308 Exibições
- Última mensagem por Guga1981

Ter Out 17, 2017 19:16
Geometria Plana
-
- integral dupla delimitada por circunferência coordenadas pol
por pri28 » Seg Dez 21, 2015 09:48
- 1 Respostas
- 3802 Exibições
- Última mensagem por Russman

Qua Dez 23, 2015 22:20
Cálculo: Limites, Derivadas e Integrais
-
- Determinação de pontos pertencentes a circunferência
por Troe » Qua Out 07, 2009 17:36
- 0 Respostas
- 1104 Exibições
- Última mensagem por Troe

Qua Out 07, 2009 17:36
Geometria Plana
-
- Circunferência, conjunto de pontos representados geometricam
 por elisamaria » Seg Jul 06, 2015 20:13
por elisamaria » Seg Jul 06, 2015 20:13
- 1 Respostas
- 1563 Exibições
- Última mensagem por nakagumahissao

Qua Ago 19, 2015 15:36
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 são conhecidos e há triângulos retângulos com as projeções:
são conhecidos e há triângulos retângulos com as projeções: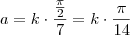
 variar em seu projeto, com
variar em seu projeto, com 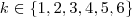 .
. da circunferência de raio
da circunferência de raio  e centro
e centro  , tal que
, tal que 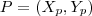 , então temos:
, então temos: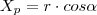

 o ângulo formado por
o ângulo formado por 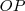 e o eixo x.
e o eixo x.