Função - linha de raciocinio

por **vmouc** » Sáb Mar 05, 2011 23:05

Por gentileza, ajude-me a entender a linha de raciocínio para resolver problemas semelhantes:

f(x)=X^2-4/x-1 , Encontrar f(1/t), f(1/2) e f(x-2).

por **vmouc** » Sáb Mar 05, 2011 23:51

Fiz o seguinte para f(x)=x^2-4/x-1
f(1/2)= (1/2)^2 - 4/(1/2)-1=
(1/4) - 4/(-1/2)=
1-16/4 / (-1/2)
-15/4 . 2 = -30/4 = 15/2

Essa linha de raciocínio está correta? Como faço no caso de f(1/t)? t^-1?

por **LuizAquino** » Dom Mar 06, 2011 09:47

Analisando a sua solução, a função do exercício é $f(x) = \frac{x^2 -4}{x - 1}$ , mas o que você escreveu foi $f(x) = x^2 - \frac{4}{x} - 1$ .

Para escrever a função que você queria na notação que você usou, então deveria ter escrito:
f(x)=(x^2-4)/(x-1)

Agora, quanto a sua solução, você está certa. Para a função original do exercício, temos que $f\left(\frac{1}{2}\right)= \frac{15}{2}$ .

Para calcular os outros valores pedidos no exercício você vai usar o mesmo procedimento. A única diferença é que você terá que fazer os cálculos de modo literal, isto é, usando incógnitas ao invés de números.

Dica
O fórum suporta o sistema LaTeX, que serve para digitar os símbolos e notações matemáticas de forma adequada. Se você ainda não estiver bem treinada no LaTeX, você pode usar o botão "Editor de Fórmulas", disponível na edição de suas mensagens.

: botao-editor-de-formulas.png (2.82 KiB) Exibido 14964 vezes

por **vmouc** » Dom Mar 06, 2011 12:10

Ok. Obrigado!
Só que não consegui resolver a questão:

$f(\frac{1}{t})=\frac{(\frac{1}{t})^2-4}{\frac{1}{t}-1}$

$f(\frac{1}{t})=\frac{\frac{1}{t^2}-4}{\frac{1}{t}-1}$

$f(\frac{1}{t})=(\frac{1}{t^2}-4).(t-1)$

$f(\frac{1}{t})=\frac{t}{t^2}-\frac{1}{t^2}-4t+4$

$f(\frac{1}{t})={t}^{-1}-{t}^{-2}-4t+4\Rightarrow-{t}^{-2}+{t}^{-1}-4t+4$

Está correto? Se não, como deveria ser feito? Onde eu errei? Se sim, como é dada a solução final?

por **vmouc** » Dom Mar 06, 2011 14:25

Pessoal, vou postar minhas dúvidas sobre funções neste tópico. Se possível, me ajudem, por gentileza!
Vou colocar a forma que encontrei de resolver e se estiver errado peço esclarecimentos.
Continuando:

$f(x)= \frac{{x}^{2}-4}{x-1}$

$f(x-2)= \frac{({x-2})^{2}-4}{x-2-1}$

$f(x-2)= \frac{{x}^{2}-4x+4-4}{x-3}$

$f(x-2)= \frac{{x}^{2}-4x}{x-3}$

$f(x-2)= ({x}^{2}-4x})({x}^{-1}-\frac{1}{3})$ ?

$f(x-2)= x-\frac{1}{3}x^2-4+\frac{4x}{3}$

$f(x-2)=- \frac{1}{3}{x}^{2}+\frac{7x}{3}-4$ ?

Acho que ja to fazendo bagunça...rsrs... me ajudem, please!

por **Renato_RJ** » Dom Mar 06, 2011 14:33

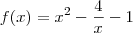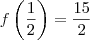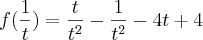
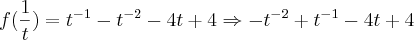
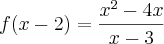
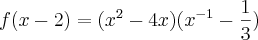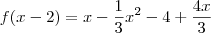
vmouc escreveu:
$f(x-2)= \left(\frac{{x}^{2}-4x}{x-3} \right)x$ ?

Está certo?

Caro Vinicius eu, pessoalmente, não entendi porque você multiplicou por x nesta passagem... Eu acho que a sua função terminava mesmo em $\frac{x^2 - 4x}{x - 3}$ .

[ ]'s
Renato.

por **vmouc** » Dom Mar 06, 2011 14:41

Tentei multiplicar todos por um fator comun para depois dividir os polinomios, mas acho que não deu certo. aí tentei denovo, da uma olhada, por favor, Renato!

[]'s

por **Renato_RJ** » Dom Mar 06, 2011 14:50

Vinicius, qual o problema da função ficar na forma de fração ?

por **vmouc** » Dom Mar 06, 2011 14:54

Pois de acordo com o professor o raciocinio estaria incompleto. E fica mais complicado encontrar "x". (Eu acho) Por isso preciso chegar até a forma mais simples e apresentar uma solução para esta função e expressá-la no gráfico.

por **Renato_RJ** » Dom Mar 06, 2011 15:27

Vinicius, então estamos errando em algo... Eu fiz uma simplificação, veja...

$\frac{x^2 - 4x}{x - 3} \Rightarrow \, \frac{(x - 2)^2}{x - 3} - \frac{4}{x - 3}$

Mas você pode desenhar um gráfico de uma fração, sem problemas algum, só que você terá, provavelmente, uma assíntota....

por **vmouc** » Dom Mar 06, 2011 15:45

Nossa, agora é q eu não entendi nada...rsrsrs....
Qual seria o valor do "x" pra esta questão?

por **Renato_RJ** » Dom Mar 06, 2011 15:59

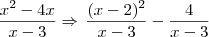
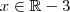Bem, eu acho que seria $x \in \mathbb{R} - {3}$ , pois se atribuirmos 3 a x, teremos o valor 0 no denominador da função, o que gera uma indeterminação...

Eu acho, posso ter me enganado...

[ ]'s
Renato.

por **vmouc** » Dom Mar 06, 2011 16:07

Na minha linha de racícionio para resolver esta questão(acima) você saberia me informar onde errei?

Obrigado!

por **vmouc** » Dom Mar 06, 2011 16:56

A questão de $f(\frac{1}{t})=$ está certa? (Veja acima)

por **LuizAquino** » Dom Mar 06, 2011 18:11

$f\left(\frac{1}{t}\right)=\frac{\left(\frac{1}{t}\right)^2-4}{\frac{1}{t}-1}$

$f\left(\frac{1}{t}\right)=\frac{\frac{1}{t^2}-4}{\frac{1}{t}-1}$

$f\left(\frac{1}{t}\right)=\frac{\frac{1-4t^2}{t^2}}{\frac{1-t}{t}}$

$f\left(\frac{1}{t}\right)=\frac{1-4t^2}{t^2} \cdot \frac{t}{1-t}$

$f\left(\frac{1}{t}\right)=\frac{1-4t^2}{t(1-t)}$

$f\left(\frac{1}{t}\right)=\frac{(1-2t)(1+2t)}{t(1-t)}$

-----------------

$f(x-2)= \frac{({x-2})^{2}-4}{x-2-1}$

$f(x-2)= \frac{{x}^{2}-4x+4-4}{x-3}$

$f(x-2)= \frac{{x}^{2}-4x}{x-3}$

$f(x-2)= \frac{x(x-4)}{x-3}$

-----------------

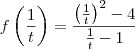
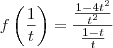
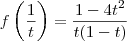
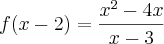
Pois de acordo com o professor o raciocínio estaria incompleto.

Qual é o texto do exercício original?

por **vmouc** » Dom Mar 06, 2011 18:20

Me refiro á deixar incognita no denominador... esta seria a solução final da função?

por **LuizAquino** » Dom Mar 06, 2011 18:59

vmouc escreveu:Me refiro á deixar incógnita no denominador... esta seria a solução final da função?

Nesses exemplos sempre teremos a variável aparecendo no denominador.

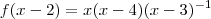Ainda que possamos escrever $f\left(\frac{1}{t}\right)=(1-2t)(1+2t)[t(1-t)]^{-1}$ e $f(x-2)= x(x-4)(x-3)^{-1}$ , essas potências negativas farão com que a variável volte a aparecer no denominador de qualquer maneira.

Observação
Na função f(x)=2x+4 a letra "x" representa uma variável, isto é, algo que pode assumir qualquer valor. Nesse caso, esses valores são aqueles no domínio da função.

Por outro lado, na equação 2x+4=0 a letra "x" representa uma incógnita, isto é, um valor desconhecido a ser determinado.

por **vmouc** » Dom Mar 06, 2011 20:18

ok. Obrigado!!!! :-D

por **vmouc** » Ter Mar 08, 2011 14:55

Boa tarde,

Pessoal,

Gostaria de saber se resolvi da forma correta:

Se $f(x)={x}^{2}+2x, determine \frac{f(a+h)-f(a)}{h}$

Resolução:
$f(a+h)= {(a+h)}^{2}+2(a+h)\Rightarrow f(a+h)={a}^{2}+2ah+{h}^{2}+2a+2h$

$f(a)={a}^{2}+2a$

$f(a+h)-f(a)= {a}^{2}-2ah+{h}^{2}+2a+2h-{a}^{2}-2a\Rightarrow f(a+h)-f(a)= {h}^{2}-2ah+2h$

$\frac{f(a+h)-f(a)}{h}= \frac{{h}^{2}-2ah+2h}{h}\Rightarrow h-2a+2$

Está correto?

Obrigado!!! :-D

por **LuizAquino** » Ter Mar 08, 2011 18:36

Procure não usar tópicos anteriores para postar novos exercícios.

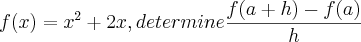
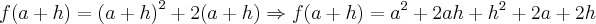
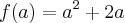
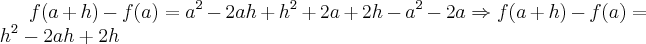
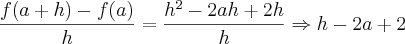
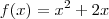Nós temos que $f(x)={x}^{2}+2x$ e queremos determinar $\frac{f(a+h)-f(a)}{h}$ . Primeiro, note que necessariamente h é diferente de 0, já que ele aparece no denominador.

$\frac{f(a+h)-f(a)}{h} = \frac{(a+h)^2+2(a+h) - a^2 - 2a}{h}$

Arrumando de forma conveniente:
$= \frac{(a+h)^2 - a^2 + 2a - 2a + 2h}{h}$

Usando o produto notável x^2-y^2=(x-y)(x+y)

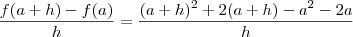
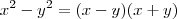e simplificando 2a com -2a:
$= \frac{(a+h- a)(a+h+a) + 2h}{h}$

$= \frac{h(2a+h) + 2h}{h}$

Colocando h em evidência:
$= \frac{h(2a+h + 2)}{h}$

Simplificando o h no numerador com o h no denominador (o que pode ser feito já que h não é zero):
= 2a+h + 2

Função - linha de raciocinio

Função - linha de raciocinio

Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Re: Função - linha de raciocinio

Quem está online