 por Thais Camerino » Sex Mai 09, 2014 12:30
por Thais Camerino » Sex Mai 09, 2014 12:30
Oi gente, queria saber como devo fazer/pensar quando este tipo de pergunta aparece, se alguém tiver a paciência de explicar, ficaria muito grata !

Que d seja a razão da progressão aritmética { an } ( n = 1, 2, 3, .... ) que satisfaça estas duas condições :
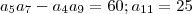
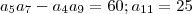
Logo,
(1) Ou
![d = \left[A \right] d = \left[A \right]](/latexrender/pictures/32c7b6a8182d5c0ec2d17f011b4fc65d.png)
ou
![d = \left[B \right] d = \left[B \right]](/latexrender/pictures/18bfb486af2b4e641a79f1acb73428bc.png)
, onde
![\left[A \right] > \left[B \right] \left[A \right] > \left[B \right]](/latexrender/pictures/3bc2b7d794dfd977166403cf2d7b8ed8.png)
.
(2) Se
![d= \left[A \right] d= \left[A \right]](/latexrender/pictures/49b29f9803b8bfe9174fede96c5df58c.png)
, então
![{a}_{1} = \left[C \right], {a}_{n} = \left[D \right]n - \left[E \right] {a}_{1} = \left[C \right], {a}_{n} = \left[D \right]n - \left[E \right]](/latexrender/pictures/97a061df86c89305b9bb4f79a206b9d9.png)
, e a somatória dos primeiros n termos é 195_ quando
![n = \left[F \right] n = \left[F \right]](/latexrender/pictures/116a4497bc47db7b09d68ac53c53f75a.png)
-
Thais Camerino
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Abr 27, 2014 00:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Design
- Andamento: cursando
 por e8group » Sex Mai 09, 2014 14:50
por e8group » Sex Mai 09, 2014 14:50
Construa a sequência ,
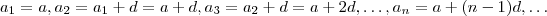
.
Onde

são numeros reais que satisfaça as condições dadas . Dá primeira eq. segue
![a_5 a_7 - a_4a_9 = 60 \iff [a + 4d][a+6d] - [a+2d][a+8d] = 60 a_5 a_7 - a_4a_9 = 60 \iff [a + 4d][a+6d] - [a+2d][a+8d] = 60](/latexrender/pictures/f41c6cd718ba2b576ce56d77b7d5ce22.png)
e dá ultima ,
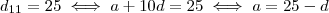
. Basta subtituir este resultado na relação enterior e determinar o

que assegura as condições .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Thais Camerino » Sáb Mai 10, 2014 01:39
por Thais Camerino » Sáb Mai 10, 2014 01:39
santhiago escreveu:Construa a sequência ,
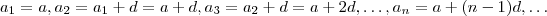
.
Onde

são numeros reais que satisfaça as condições dadas . Dá primeira eq. segue
![a_5 a_7 - a_4a_9 = 60 \iff [a + 4d][a+6d] - [a+2d][a+8d] = 60 a_5 a_7 - a_4a_9 = 60 \iff [a + 4d][a+6d] - [a+2d][a+8d] = 60](/latexrender/pictures/f41c6cd718ba2b576ce56d77b7d5ce22.png)
e dá ultima ,
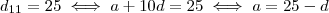
. Basta subtituir este resultado na relação enterior e determinar o

que assegura as condições .
eu tinha montado essa equação mas ao desenvolve-la, não deu o resultado correto :s Na seguinte :
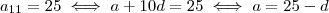
Como o 10 desapareceu?
-
Thais Camerino
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Abr 27, 2014 00:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Design
- Andamento: cursando
 por e8group » Sáb Mai 10, 2014 10:38
por e8group » Sáb Mai 10, 2014 10:38
Erro de digitação . Consegue avançar ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Thais Camerino » Sáb Mai 10, 2014 13:21
por Thais Camerino » Sáb Mai 10, 2014 13:21
Acho que deu erro na sua mensagem Santhiago
-
Thais Camerino
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Abr 27, 2014 00:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Design
- Andamento: cursando
 por e8group » Sáb Mai 10, 2014 20:02
por e8group » Sáb Mai 10, 2014 20:02
Sim , como já mencionei erro de digitação .
corrigindo :

e

. Disso temos que

. Das duas uma , substitua
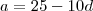
ou o próprio

. Como prossegue ,
![a +4d = a + 10d -6d = [a+10d] -6d = 25 -6d a +4d = a + 10d -6d = [a+10d] -6d = 25 -6d](/latexrender/pictures/118b514345b8cafff3e15db5f8c9abba.png)
![a + 6d = a + 10d - 4d = [a +10d] -4d = 25 -4d a + 6d = a + 10d - 4d = [a +10d] -4d = 25 -4d](/latexrender/pictures/b1176854d67c41b9e32705500ca2105b.png)
e assim por diante . Depois cabe a analisar a(s) solução(oes) de para d que satisfaz os dados .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Thais Camerino » Ter Mai 13, 2014 13:52
por Thais Camerino » Ter Mai 13, 2014 13:52
Supostamente ficaria assim a equação :
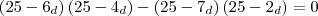
.... ?
Quando fiz não deu o resultado correto.. Na solução aparece o seguinte:
d = 4 ou d =

a = - 15
an =

- 19
n = 15
Desculpa eu sei que é chato explicar algo pra alguém e ela não perceber.. mas não estou chegando la :s
-
Thais Camerino
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Abr 27, 2014 00:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Design
- Andamento: cursando
 por e8group » Ter Mai 13, 2014 14:32
por e8group » Ter Mai 13, 2014 14:32
Quase !
Vamos lá :

n=1,2,3... .
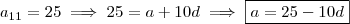
(i) . Agora , do enunciado
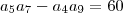
,i.e,
![[a + 4d][a +6d] - [a + 3d][a +8d] = 60 [a + 4d][a +6d] - [a + 3d][a +8d] = 60](/latexrender/pictures/dfea7b14d07935fae139bde43737c8ae.png)
(Aqui substituirmos cada termo

pelo seu correspondente
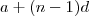
( n = 5,7,4,9 ) (ii)
Substituindo (i) em (ii) , ficamos com
![[ (25 - 10d)+ 4d][(25 - 10d) +6d] - [(25 - 10d) + 3d][(25 - 10d) +8d] = 60 \iff [ (25 - 10d)+ 4d][(25 - 10d) +6d] - [(25 - 10d) + 3d][(25 - 10d) +8d] = 60 \iff](/latexrender/pictures/6b91a883d15dbef9049295a44496dc9e.png)
![[25-6d][25-4d] - [25 -7d][25 -2d] = 60 [25-6d][25-4d] - [25 -7d][25 -2d] = 60](/latexrender/pictures/9821875aca370fb0b4d25d4c1809dce7.png)
(A sua eq. está correta )
Aplicando a distributiva e simplificando obtemos a equação
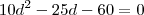
que nos dá graças a fórmula resolvente
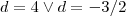
como solução da equação .
Para cada valor de

acima (que satisfaz
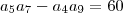
) é possível encontrar um

correspondente que satisfaz

, e assim ambas condições serão estabelecidas . Temos então duas possíveis sequências (P.A) que satisfaz as condições do enunciado .
Não encontrasse estes valores ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Thais Camerino » Ter Mai 13, 2014 18:51
por Thais Camerino » Ter Mai 13, 2014 18:51
Aaah! Finalmente consegui!! Muito obrigada!!! Obrigada pela paciência !!

-
Thais Camerino
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Abr 27, 2014 00:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Design
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6135 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4726 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5630 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4425 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8399 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

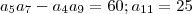
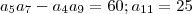
![d = \left[A \right] d = \left[A \right]](/latexrender/pictures/32c7b6a8182d5c0ec2d17f011b4fc65d.png) ou
ou ![d = \left[B \right] d = \left[B \right]](/latexrender/pictures/18bfb486af2b4e641a79f1acb73428bc.png) , onde
, onde![\left[A \right] > \left[B \right] \left[A \right] > \left[B \right]](/latexrender/pictures/3bc2b7d794dfd977166403cf2d7b8ed8.png) .
. ![d= \left[A \right] d= \left[A \right]](/latexrender/pictures/49b29f9803b8bfe9174fede96c5df58c.png) , então
, então ![{a}_{1} = \left[C \right], {a}_{n} = \left[D \right]n - \left[E \right] {a}_{1} = \left[C \right], {a}_{n} = \left[D \right]n - \left[E \right]](/latexrender/pictures/97a061df86c89305b9bb4f79a206b9d9.png) , e a somatória dos primeiros n termos é 195_ quando
, e a somatória dos primeiros n termos é 195_ quando ![n = \left[F \right] n = \left[F \right]](/latexrender/pictures/116a4497bc47db7b09d68ac53c53f75a.png)


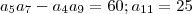
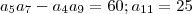
![d = \left[A \right] d = \left[A \right]](/latexrender/pictures/32c7b6a8182d5c0ec2d17f011b4fc65d.png) ou
ou ![d = \left[B \right] d = \left[B \right]](/latexrender/pictures/18bfb486af2b4e641a79f1acb73428bc.png) , onde
, onde![\left[A \right] > \left[B \right] \left[A \right] > \left[B \right]](/latexrender/pictures/3bc2b7d794dfd977166403cf2d7b8ed8.png) .
. ![d= \left[A \right] d= \left[A \right]](/latexrender/pictures/49b29f9803b8bfe9174fede96c5df58c.png) , então
, então ![{a}_{1} = \left[C \right], {a}_{n} = \left[D \right]n - \left[E \right] {a}_{1} = \left[C \right], {a}_{n} = \left[D \right]n - \left[E \right]](/latexrender/pictures/97a061df86c89305b9bb4f79a206b9d9.png) , e a somatória dos primeiros n termos é 195_ quando
, e a somatória dos primeiros n termos é 195_ quando ![n = \left[F \right] n = \left[F \right]](/latexrender/pictures/116a4497bc47db7b09d68ac53c53f75a.png)

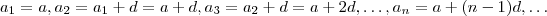 .
.  são numeros reais que satisfaça as condições dadas . Dá primeira eq. segue
são numeros reais que satisfaça as condições dadas . Dá primeira eq. segue ![a_5 a_7 - a_4a_9 = 60 \iff [a + 4d][a+6d] - [a+2d][a+8d] = 60 a_5 a_7 - a_4a_9 = 60 \iff [a + 4d][a+6d] - [a+2d][a+8d] = 60](/latexrender/pictures/f41c6cd718ba2b576ce56d77b7d5ce22.png) e dá ultima ,
e dá ultima , 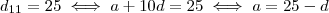 . Basta subtituir este resultado na relação enterior e determinar o
. Basta subtituir este resultado na relação enterior e determinar o  que assegura as condições .
que assegura as condições .
.
são numeros reais que satisfaça as condições dadas . Dá primeira eq. segue
e dá ultima ,
. Basta subtituir este resultado na relação enterior e determinar o
que assegura as condições .
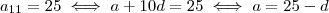 Como o 10 desapareceu?
Como o 10 desapareceu?


 e
e  . Disso temos que
. Disso temos que  . Das duas uma , substitua
. Das duas uma , substitua 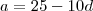 ou o próprio
ou o próprio  . Como prossegue ,
. Como prossegue , ![a +4d = a + 10d -6d = [a+10d] -6d = 25 -6d a +4d = a + 10d -6d = [a+10d] -6d = 25 -6d](/latexrender/pictures/118b514345b8cafff3e15db5f8c9abba.png)
![a + 6d = a + 10d - 4d = [a +10d] -4d = 25 -4d a + 6d = a + 10d - 4d = [a +10d] -4d = 25 -4d](/latexrender/pictures/b1176854d67c41b9e32705500ca2105b.png) e assim por diante . Depois cabe a analisar a(s) solução(oes) de para d que satisfaz os dados .
e assim por diante . Depois cabe a analisar a(s) solução(oes) de para d que satisfaz os dados .
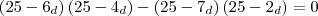 .... ?
.... ? 
 - 19
- 19
 n=1,2,3... .
n=1,2,3... . 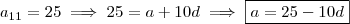 (i) . Agora , do enunciado
(i) . Agora , do enunciado 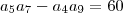 ,i.e,
,i.e, ![[a + 4d][a +6d] - [a + 3d][a +8d] = 60 [a + 4d][a +6d] - [a + 3d][a +8d] = 60](/latexrender/pictures/dfea7b14d07935fae139bde43737c8ae.png) (Aqui substituirmos cada termo
(Aqui substituirmos cada termo  pelo seu correspondente
pelo seu correspondente 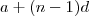 ( n = 5,7,4,9 ) (ii)
( n = 5,7,4,9 ) (ii) ![[ (25 - 10d)+ 4d][(25 - 10d) +6d] - [(25 - 10d) + 3d][(25 - 10d) +8d] = 60 \iff [ (25 - 10d)+ 4d][(25 - 10d) +6d] - [(25 - 10d) + 3d][(25 - 10d) +8d] = 60 \iff](/latexrender/pictures/6b91a883d15dbef9049295a44496dc9e.png)
![[25-6d][25-4d] - [25 -7d][25 -2d] = 60 [25-6d][25-4d] - [25 -7d][25 -2d] = 60](/latexrender/pictures/9821875aca370fb0b4d25d4c1809dce7.png) (A sua eq. está correta )
(A sua eq. está correta ) 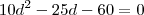 que nos dá graças a fórmula resolvente
que nos dá graças a fórmula resolvente 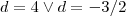 como solução da equação .
como solução da equação . acima (que satisfaz
acima (que satisfaz 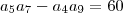 ) é possível encontrar um
) é possível encontrar um  correspondente que satisfaz
correspondente que satisfaz  , e assim ambas condições serão estabelecidas . Temos então duas possíveis sequências (P.A) que satisfaz as condições do enunciado .
, e assim ambas condições serão estabelecidas . Temos então duas possíveis sequências (P.A) que satisfaz as condições do enunciado .







