
Que d seja a razão da progressão aritmética { an } ( n = 1, 2, 3, .... ) que satisfaça estas duas condições :
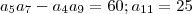
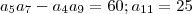
Logo,
(1) Ou
![d = \left[A \right] d = \left[A \right]](/latexrender/pictures/32c7b6a8182d5c0ec2d17f011b4fc65d.png) ou
ou ![d = \left[B \right] d = \left[B \right]](/latexrender/pictures/18bfb486af2b4e641a79f1acb73428bc.png) , onde
, onde![\left[A \right] > \left[B \right] \left[A \right] > \left[B \right]](/latexrender/pictures/3bc2b7d794dfd977166403cf2d7b8ed8.png) .
. (2) Se
![d= \left[A \right] d= \left[A \right]](/latexrender/pictures/49b29f9803b8bfe9174fede96c5df58c.png) , então
, então ![{a}_{1} = \left[C \right], {a}_{n} = \left[D \right]n - \left[E \right] {a}_{1} = \left[C \right], {a}_{n} = \left[D \right]n - \left[E \right]](/latexrender/pictures/97a061df86c89305b9bb4f79a206b9d9.png) , e a somatória dos primeiros n termos é 195_ quando
, e a somatória dos primeiros n termos é 195_ quando ![n = \left[F \right] n = \left[F \right]](/latexrender/pictures/116a4497bc47db7b09d68ac53c53f75a.png)


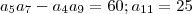
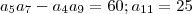
![d = \left[A \right] d = \left[A \right]](/latexrender/pictures/32c7b6a8182d5c0ec2d17f011b4fc65d.png) ou
ou ![d = \left[B \right] d = \left[B \right]](/latexrender/pictures/18bfb486af2b4e641a79f1acb73428bc.png) , onde
, onde![\left[A \right] > \left[B \right] \left[A \right] > \left[B \right]](/latexrender/pictures/3bc2b7d794dfd977166403cf2d7b8ed8.png) .
. ![d= \left[A \right] d= \left[A \right]](/latexrender/pictures/49b29f9803b8bfe9174fede96c5df58c.png) , então
, então ![{a}_{1} = \left[C \right], {a}_{n} = \left[D \right]n - \left[E \right] {a}_{1} = \left[C \right], {a}_{n} = \left[D \right]n - \left[E \right]](/latexrender/pictures/97a061df86c89305b9bb4f79a206b9d9.png) , e a somatória dos primeiros n termos é 195_ quando
, e a somatória dos primeiros n termos é 195_ quando ![n = \left[F \right] n = \left[F \right]](/latexrender/pictures/116a4497bc47db7b09d68ac53c53f75a.png)

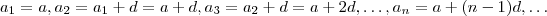 .
.  são numeros reais que satisfaça as condições dadas . Dá primeira eq. segue
são numeros reais que satisfaça as condições dadas . Dá primeira eq. segue ![a_5 a_7 - a_4a_9 = 60 \iff [a + 4d][a+6d] - [a+2d][a+8d] = 60 a_5 a_7 - a_4a_9 = 60 \iff [a + 4d][a+6d] - [a+2d][a+8d] = 60](/latexrender/pictures/f41c6cd718ba2b576ce56d77b7d5ce22.png) e dá ultima ,
e dá ultima , 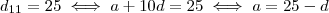 . Basta subtituir este resultado na relação enterior e determinar o
. Basta subtituir este resultado na relação enterior e determinar o  que assegura as condições .
que assegura as condições .
santhiago escreveu:Construa a sequência ,.
Ondesão numeros reais que satisfaça as condições dadas . Dá primeira eq. segue
e dá ultima ,
. Basta subtituir este resultado na relação enterior e determinar o
que assegura as condições .
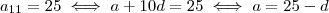 Como o 10 desapareceu?
Como o 10 desapareceu?


 e
e  . Disso temos que
. Disso temos que  . Das duas uma , substitua
. Das duas uma , substitua 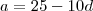 ou o próprio
ou o próprio  . Como prossegue ,
. Como prossegue , ![a +4d = a + 10d -6d = [a+10d] -6d = 25 -6d a +4d = a + 10d -6d = [a+10d] -6d = 25 -6d](/latexrender/pictures/118b514345b8cafff3e15db5f8c9abba.png)
![a + 6d = a + 10d - 4d = [a +10d] -4d = 25 -4d a + 6d = a + 10d - 4d = [a +10d] -4d = 25 -4d](/latexrender/pictures/b1176854d67c41b9e32705500ca2105b.png) e assim por diante . Depois cabe a analisar a(s) solução(oes) de para d que satisfaz os dados .
e assim por diante . Depois cabe a analisar a(s) solução(oes) de para d que satisfaz os dados .
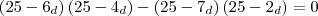 .... ?
.... ? 
 - 19
- 19
 n=1,2,3... .
n=1,2,3... . 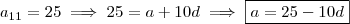 (i) . Agora , do enunciado
(i) . Agora , do enunciado 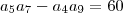 ,i.e,
,i.e, ![[a + 4d][a +6d] - [a + 3d][a +8d] = 60 [a + 4d][a +6d] - [a + 3d][a +8d] = 60](/latexrender/pictures/dfea7b14d07935fae139bde43737c8ae.png) (Aqui substituirmos cada termo
(Aqui substituirmos cada termo  pelo seu correspondente
pelo seu correspondente 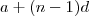 ( n = 5,7,4,9 ) (ii)
( n = 5,7,4,9 ) (ii) ![[ (25 - 10d)+ 4d][(25 - 10d) +6d] - [(25 - 10d) + 3d][(25 - 10d) +8d] = 60 \iff [ (25 - 10d)+ 4d][(25 - 10d) +6d] - [(25 - 10d) + 3d][(25 - 10d) +8d] = 60 \iff](/latexrender/pictures/6b91a883d15dbef9049295a44496dc9e.png)
![[25-6d][25-4d] - [25 -7d][25 -2d] = 60 [25-6d][25-4d] - [25 -7d][25 -2d] = 60](/latexrender/pictures/9821875aca370fb0b4d25d4c1809dce7.png) (A sua eq. está correta )
(A sua eq. está correta ) 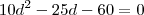 que nos dá graças a fórmula resolvente
que nos dá graças a fórmula resolvente 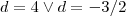 como solução da equação .
como solução da equação . acima (que satisfaz
acima (que satisfaz 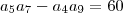 ) é possível encontrar um
) é possível encontrar um  correspondente que satisfaz
correspondente que satisfaz  , e assim ambas condições serão estabelecidas . Temos então duas possíveis sequências (P.A) que satisfaz as condições do enunciado .
, e assim ambas condições serão estabelecidas . Temos então duas possíveis sequências (P.A) que satisfaz as condições do enunciado .


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.