+
+
Olá pessoal!
Há dias agora estou me debatendo com o seguinte problema:
Mostre que
Det[M={{1, cos(2a), sen(a)}, {1, cos(2b), sen(b)}, {1, cos(2c), sen(c)}}]
é igual a
2*[sen(b)-sen(c)]*[sen(c)-sen(a)]*[sen(a)-sen(b)]
Eu só consigo chegar a
cos(2a)sen(b)-cos(2a)sen(c)+cos(2b)sen(c)-cos(2b)sen(a)+ cos(2c)sen(a)-cos(2c)sen(b)
ou cos(2a)[sen(b)-sen(c)] + cos(2b)[sen(c)-sen(a)] + cos(2c)[sen(a)-sen(b)]
Agora como transformar esta SOMA em um PRODUTO me escapa completamente, já consumi diversas “arvores” sem resultados....
Nota: Inserindo valores consegui ao menos constatar que a SOMA e o PRODUTO dão o mesmo resultado...
Alguém aí pode me dar uma orientação?
Colton
+
+


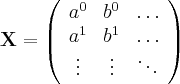
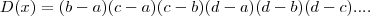 .Agora você deve estar se perguntando "Que 'c' e 'd' são esses?",eles são os outros elementos da mesma linha de a e de b,no exemplo estão em ordem alfabética.O mecanismo para calcular o determinante é ir diminuindo,um a um, os algarismos que estão a esquerda do numero do qual eles serão diminuidos.
.Agora você deve estar se perguntando "Que 'c' e 'd' são esses?",eles são os outros elementos da mesma linha de a e de b,no exemplo estão em ordem alfabética.O mecanismo para calcular o determinante é ir diminuindo,um a um, os algarismos que estão a esquerda do numero do qual eles serão diminuidos. e como o determinante de uma matriz 1x1 é o elemento da matriz
e como o determinante de uma matriz 1x1 é o elemento da matriz 
![Cos(2x)={[cos(x)]}^{2}-{[sen(x)]}^{2}=2{[cos(x)]}^{2}-1=1-2{[sen(x)]}^{2} Cos(2x)={[cos(x)]}^{2}-{[sen(x)]}^{2}=2{[cos(x)]}^{2}-1=1-2{[sen(x)]}^{2}](/latexrender/pictures/419c705d39293fa36891d4c5e3a1baf3.png)
 , se tudo der certo aprenderei ano que vem.
, se tudo der certo aprenderei ano que vem.


 .
.



