10-)(efomm) dados A={2,3,4},B={1,6,8,12} A relação R={(x,y) e AxB / y=x+4} de A em B é dada por:
a-){(3,6);(4,8)}
b-){(2,6);(4,8)}
c-){(6,2);(8,4)}
d-){(2,6);(3,12);(4,8)}
e-){(2,1);(3,6);(4,8)}
obs: esse "e" no meio acho que é pertence R={(x,y) e AxB
não conseguir fazer
valew


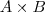 lê-se como
lê-se como  produto cartesiano
produto cartesiano  , ou simplesmente
, ou simplesmente 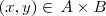 , o
, o  pertence a
pertence a  pertence a
pertence a 


 .
.
 :
: