 por 404040 » Seg Out 18, 2010 18:27
por 404040 » Seg Out 18, 2010 18:27
Se nº 111 for dividido em três partes, que constituem uma PG de razão 3/4, a menor desssas partes será :
Estou quebrando a cabeça mas não consigo nem começar o cálculo...
-
404040
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 17, 2010 20:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por VtinxD » Sáb Out 23, 2010 03:18
por VtinxD » Sáb Out 23, 2010 03:18
Podemos escrever uma PG desta forma:
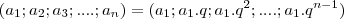
.Sendo

o termo independente ,

o n-ésimo termo e "q" a razão da PG.
Como o numero 111 foi dividido em três partes em PG logo podem ser escritos da for utilizada acima ,como são apenas 3 números em PG podemos utilizar os tres primeiros termos da dela.

.Como
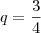
temos:

.Tirando o mmc:

Como a PG é decrecente, graças a sua razão menor do que 1,o menor termo não é

e sim
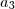
.
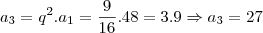
Espero ter ajudado e me desculpe qualquer erro mas são 3 da manhã

.Boa noite
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por 404040 » Sáb Out 23, 2010 09:21
por 404040 » Sáb Out 23, 2010 09:21
Agradeço muito a boa vontade, principalmente neste horário, sua explicação foi ótima, simples e prática, valeu...
-
404040
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 17, 2010 20:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



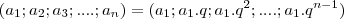 .Sendo
.Sendo  o termo independente ,
o termo independente ,  o n-ésimo termo e "q" a razão da PG.
o n-ésimo termo e "q" a razão da PG. .Como
.Como 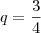 temos:
temos: .Tirando o mmc:
.Tirando o mmc:
 e sim
e sim 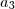 .
.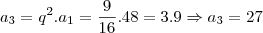
 .Boa noite
.Boa noite