 por natanskt » Seg Out 11, 2010 16:23
por natanskt » Seg Out 11, 2010 16:23
1-)(ESPCEX) sendo
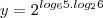
o valor de y é
a-)2
b-)5
c-)6
d-)12
e-)30
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por MarceloFantini » Seg Out 11, 2010 16:57
por MarceloFantini » Seg Out 11, 2010 16:57

Pela propriedade da mudança de base, temos:

. Portanto:
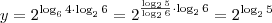
Pela propriedade que diz que
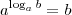
, resulta em:

Alternativa B.
Natanskt, já percebi que você posta muitas questões com o mesmo método de resolução, praticamente todas apenas cobram o uso de propriedades. Você precisa estudar as respostas dadas aqui no fórum e
REFAZÊ-LAS sozinho para aprender de verdade, e tentar fazer antes de tudo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por natanskt » Seg Out 11, 2010 17:16
por natanskt » Seg Out 11, 2010 17:16
ta bom!!
é que eu tento fazer,e não consigo...
estou com muita dificuldade em aprender essa matéria,se eu tivesse um professor estaria melhor,é que eu to tentando aprender sozinho
depois que eu vejo a resposta eu aprendo,mais quando tem outra questão eu fico perdido dinovo,
valeu !!!!
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por DanielRJ » Seg Out 11, 2010 18:39
por DanielRJ » Seg Out 11, 2010 18:39
natanskt escreveu:ta bom!!
é que eu tento fazer,e não consigo...
estou com muita dificuldade em aprender essa matéria,se eu tivesse um professor estaria melhor,é que eu to tentando aprender sozinho
depois que eu vejo a resposta eu aprendo,mais quando tem outra questão eu fico perdido dinovo,
valeu !!!!
Vai no youtube. e procura por "aulasdematematica" entra nesse canal. tem um professor que ele ensina perfeitamente essa materia boa sorte.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:16
- 3 Respostas
- 2187 Exibições
- Última mensagem por MarceloFantini

Qua Out 13, 2010 13:50
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:50
- 2 Respostas
- 5659 Exibições
- Última mensagem por DanielRJ

Seg Out 11, 2010 18:25
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:53
- 3 Respostas
- 2949 Exibições
- Última mensagem por MarceloFantini

Qui Out 14, 2010 16:38
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Qua Out 13, 2010 18:09
- 2 Respostas
- 4841 Exibições
- Última mensagem por gustavofr

Qui Out 28, 2010 09:19
Logaritmos
-
- (ESPCEX) função logaritmica
por natanskt » Sex Out 29, 2010 10:34
- 1 Respostas
- 1576 Exibições
- Última mensagem por SidneySantos

Qua Abr 20, 2011 20:36
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
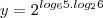 o valor de y é
o valor de y é
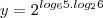 o valor de y é
o valor de y é

 . Portanto:
. Portanto: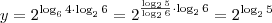
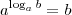 , resulta em:
, resulta em:




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.