 por natanskt » Sex Out 08, 2010 12:27
por natanskt » Sex Out 08, 2010 12:27
O valor de
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right] -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]](/latexrender/pictures/61c2f277bbcd3808f546e74a4cd4872a.png)
é?
a-)1
b-)2
c-)3
d-)4
nem conseguir começar a conta
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por DanielRJ » Sex Out 08, 2010 14:25
por DanielRJ » Sex Out 08, 2010 14:25
natanskt escreveu:O valor de
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right] -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]](/latexrender/pictures/61c2f277bbcd3808f546e74a4cd4872a.png)
é?
a-)1
b-)2
c-)3
d-)4
nem conseguir começar a conta
![-log_{2}[log_{2}2^\frac{1}{8}] -log_{2}[log_{2}2^\frac{1}{8}]](/latexrender/pictures/39755266c310f4f95e7b7b9b478f4a82.png)
cortas o 2 da base e o 2 logaritmano.
![-log_{2}[\frac{1}{8}] -log_{2}[\frac{1}{8}]](/latexrender/pictures/711b9dd000d1a570719aca1b31e5304d.png)
![-log_{2}[\frac{1}{2^3}] -log_{2}[\frac{1}{2^3}]](/latexrender/pictures/b112a02bae6f1e248ee980861cf8caee.png)

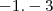

Eu fiquei meio em duvida vamo esperar algum amigo aparecer ai..
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sex Out 08, 2010 14:30
por Molina » Sex Out 08, 2010 14:30
natanskt escreveu:O valor de
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right] -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]](/latexrender/pictures/61c2f277bbcd3808f546e74a4cd4872a.png)
é?
a-)1
b-)2
c-)3
d-)4
nem conseguir começar a conta
Boa tarde, Natan.
Vamos resolvendo por partes:
Sabemos que

Ou seja,
![\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=\left[log_2 2^{\frac{1}{8}} \right]=\frac{1}{8}*log_2 2 =\frac{1}{8}*1=\frac{1}{8} \left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=\left[log_2 2^{\frac{1}{8}} \right]=\frac{1}{8}*log_2 2 =\frac{1}{8}*1=\frac{1}{8}](/latexrender/pictures/2a6b0407843168668ea22ef38fb50a49.png)
Voltando na expressão geral:
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=-log_2\left[\frac{1}{8} \right]=-log_2\left[2^{-3} \right]=-(-3)*log_2 2 =3*1=3 -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=-log_2\left[\frac{1}{8} \right]=-log_2\left[2^{-3} \right]=-(-3)*log_2 2 =3*1=3](/latexrender/pictures/d8a33381f99ad26c86d4bd1537c9d1e3.png)
Basicamente foi usado as propriedades logarítmicas e algébricas.
Qualquer dúvida em alguma passagem, informe!
Bom estudo.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação logaritmica
por DanielRJ » Qui Out 07, 2010 17:20
- 4 Respostas
- 2460 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 15:28
Logaritmos
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:30
- 1 Respostas
- 1456 Exibições
- Última mensagem por DanielRJ

Sex Out 08, 2010 14:13
Funções
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 13:31
- 1 Respostas
- 1674 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 13:42
Logaritmos
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 14:51
- 2 Respostas
- 1821 Exibições
- Última mensagem por natanskt

Seg Out 11, 2010 15:58
Logaritmos
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 15:00
- 1 Respostas
- 1638 Exibições
- Última mensagem por Douglasm

Sáb Out 09, 2010 17:29
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right] -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]](/latexrender/pictures/61c2f277bbcd3808f546e74a4cd4872a.png) é?
é?
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right] -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]](/latexrender/pictures/61c2f277bbcd3808f546e74a4cd4872a.png) é?
é?
é?
![-log_{2}[log_{2}2^\frac{1}{8}] -log_{2}[log_{2}2^\frac{1}{8}]](/latexrender/pictures/39755266c310f4f95e7b7b9b478f4a82.png) cortas o 2 da base e o 2 logaritmano.
cortas o 2 da base e o 2 logaritmano.![-log_{2}[\frac{1}{8}] -log_{2}[\frac{1}{8}]](/latexrender/pictures/711b9dd000d1a570719aca1b31e5304d.png)
![-log_{2}[\frac{1}{2^3}] -log_{2}[\frac{1}{2^3}]](/latexrender/pictures/b112a02bae6f1e248ee980861cf8caee.png)

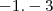


é?

![\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=\left[log_2 2^{\frac{1}{8}} \right]=\frac{1}{8}*log_2 2 =\frac{1}{8}*1=\frac{1}{8} \left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=\left[log_2 2^{\frac{1}{8}} \right]=\frac{1}{8}*log_2 2 =\frac{1}{8}*1=\frac{1}{8}](/latexrender/pictures/2a6b0407843168668ea22ef38fb50a49.png)
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=-log_2\left[\frac{1}{8} \right]=-log_2\left[2^{-3} \right]=-(-3)*log_2 2 =3*1=3 -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=-log_2\left[\frac{1}{8} \right]=-log_2\left[2^{-3} \right]=-(-3)*log_2 2 =3*1=3](/latexrender/pictures/d8a33381f99ad26c86d4bd1537c9d1e3.png)

