 por natanskt » Sex Out 08, 2010 12:27
por natanskt » Sex Out 08, 2010 12:27
O valor de
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right] -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]](/latexrender/pictures/61c2f277bbcd3808f546e74a4cd4872a.png)
é?
a-)1
b-)2
c-)3
d-)4
nem conseguir começar a conta
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por DanielRJ » Sex Out 08, 2010 14:25
por DanielRJ » Sex Out 08, 2010 14:25
natanskt escreveu:O valor de
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right] -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]](/latexrender/pictures/61c2f277bbcd3808f546e74a4cd4872a.png)
é?
a-)1
b-)2
c-)3
d-)4
nem conseguir começar a conta
![-log_{2}[log_{2}2^\frac{1}{8}] -log_{2}[log_{2}2^\frac{1}{8}]](/latexrender/pictures/39755266c310f4f95e7b7b9b478f4a82.png)
cortas o 2 da base e o 2 logaritmano.
![-log_{2}[\frac{1}{8}] -log_{2}[\frac{1}{8}]](/latexrender/pictures/711b9dd000d1a570719aca1b31e5304d.png)
![-log_{2}[\frac{1}{2^3}] -log_{2}[\frac{1}{2^3}]](/latexrender/pictures/b112a02bae6f1e248ee980861cf8caee.png)

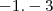

Eu fiquei meio em duvida vamo esperar algum amigo aparecer ai..
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sex Out 08, 2010 14:30
por Molina » Sex Out 08, 2010 14:30
natanskt escreveu:O valor de
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right] -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]](/latexrender/pictures/61c2f277bbcd3808f546e74a4cd4872a.png)
é?
a-)1
b-)2
c-)3
d-)4
nem conseguir começar a conta
Boa tarde, Natan.
Vamos resolvendo por partes:
Sabemos que

Ou seja,
![\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=\left[log_2 2^{\frac{1}{8}} \right]=\frac{1}{8}*log_2 2 =\frac{1}{8}*1=\frac{1}{8} \left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=\left[log_2 2^{\frac{1}{8}} \right]=\frac{1}{8}*log_2 2 =\frac{1}{8}*1=\frac{1}{8}](/latexrender/pictures/2a6b0407843168668ea22ef38fb50a49.png)
Voltando na expressão geral:
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=-log_2\left[\frac{1}{8} \right]=-log_2\left[2^{-3} \right]=-(-3)*log_2 2 =3*1=3 -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=-log_2\left[\frac{1}{8} \right]=-log_2\left[2^{-3} \right]=-(-3)*log_2 2 =3*1=3](/latexrender/pictures/d8a33381f99ad26c86d4bd1537c9d1e3.png)
Basicamente foi usado as propriedades logarítmicas e algébricas.
Qualquer dúvida em alguma passagem, informe!
Bom estudo.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação logaritmica
por DanielRJ » Qui Out 07, 2010 17:20
- 4 Respostas
- 2468 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 15:28
Logaritmos
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:30
- 1 Respostas
- 1461 Exibições
- Última mensagem por DanielRJ

Sex Out 08, 2010 14:13
Funções
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 13:31
- 1 Respostas
- 1676 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 13:42
Logaritmos
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 14:51
- 2 Respostas
- 1824 Exibições
- Última mensagem por natanskt

Seg Out 11, 2010 15:58
Logaritmos
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 15:00
- 1 Respostas
- 1639 Exibições
- Última mensagem por Douglasm

Sáb Out 09, 2010 17:29
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right] -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]](/latexrender/pictures/61c2f277bbcd3808f546e74a4cd4872a.png) é?
é?
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right] -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]](/latexrender/pictures/61c2f277bbcd3808f546e74a4cd4872a.png) é?
é?
é?
![-log_{2}[log_{2}2^\frac{1}{8}] -log_{2}[log_{2}2^\frac{1}{8}]](/latexrender/pictures/39755266c310f4f95e7b7b9b478f4a82.png) cortas o 2 da base e o 2 logaritmano.
cortas o 2 da base e o 2 logaritmano.![-log_{2}[\frac{1}{8}] -log_{2}[\frac{1}{8}]](/latexrender/pictures/711b9dd000d1a570719aca1b31e5304d.png)
![-log_{2}[\frac{1}{2^3}] -log_{2}[\frac{1}{2^3}]](/latexrender/pictures/b112a02bae6f1e248ee980861cf8caee.png)

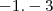


é?

![\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=\left[log_2 2^{\frac{1}{8}} \right]=\frac{1}{8}*log_2 2 =\frac{1}{8}*1=\frac{1}{8} \left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=\left[log_2 2^{\frac{1}{8}} \right]=\frac{1}{8}*log_2 2 =\frac{1}{8}*1=\frac{1}{8}](/latexrender/pictures/2a6b0407843168668ea22ef38fb50a49.png)
![-log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=-log_2\left[\frac{1}{8} \right]=-log_2\left[2^{-3} \right]=-(-3)*log_2 2 =3*1=3 -log_2\left[log_2 \sqrt { \sqrt{\sqrt{2}}} \right]=-log_2\left[\frac{1}{8} \right]=-log_2\left[2^{-3} \right]=-(-3)*log_2 2 =3*1=3](/latexrender/pictures/d8a33381f99ad26c86d4bd1537c9d1e3.png)




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.