Tenho a seguinte questão:"Use a fórmula
 para calcular a integral
para calcular a integral 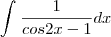 "
"Eu não estou conseguindo resolver, nunca resolvi nenhuma com sen².
A outra duvida é na seguinte questão: "Calcular a área da região delimitada por
 e
e  ,
,  e
e  .Apresente o gráfico da região desenvolvido em um software gráfico."
.Apresente o gráfico da região desenvolvido em um software gráfico."O Grafico:

Resultados que obtive:

Porem, área até onde sei tem que ser diferente de 0, alguém pode me explicar o que ha de errado?
Obrigado, Deivid Steffens.



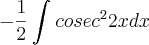 e segundo a tabela que eu tenho a resolução para essa integral se da da seguinte forma:
e segundo a tabela que eu tenho a resolução para essa integral se da da seguinte forma: 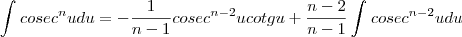 , porém, se eu aplicar a formula, terão varios valores iguais a 0. Como procedo depois de fazer o que você falou?
, porém, se eu aplicar a formula, terão varios valores iguais a 0. Como procedo depois de fazer o que você falou?
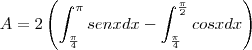


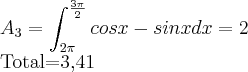




 , avisa que eu resolvo.
, avisa que eu resolvo.

