por Deivid » Ter Set 21, 2010 18:07
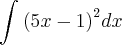por dois métodos: Primeiro elevando ao quadrado e integrando cada termo e depois fazendo a substituição u = 5 x ? 1 . Explique por que as duas respostas aparentemente diferentes, são
e segundo utilizando o método de substituição 
. Eu não consigo achar o por que delas serem equivalentes.
por Molina » Ter Set 21, 2010 18:35
Deivid escreveu:Olá usuários do fórum Ajuda Matemática, venho por meio dessa mensagem pedir ajuda em uma questão de Calculo II, não sei se é difícil, mas eu simplesmente não consigo enxergar a resposta.
"Calcule a integral
realmente equivalentes."
Eu obtive as seguintes respostas, primeiro
Obrigado.
e compare ao primeiro resultado.
por Deivid » Qua Set 22, 2010 14:29
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)