Questões simples mas não estou chegando ao resultado correto.
Obrigada! (1) Quantas são as palavras de 4 letras, formadas apenas por vogais, que têm exatamente duas letras iguais?
(a) 60 / (b) 120 / (c) 130 / (d) 240 / (e) 360
Pq e) 360 e não a) 60 ??
(2) Uma placa de um carro brasileira é uma seqüência de três letras seguidas de quatros algarismos (LETRA LETRA LETRA – ALGARISMO ALGARISMO ALGARISMO ALGARISMO). Dispõe-se 26 letras distintas e dez algarismos distintos para a confecção das placas. Quantas placas podem ser confeccionadas de modo que comece sempre com B e R nessa ordem?
Minha resposta foi
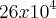, mas a resposta correta é 
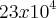. Não entendi pq 23 e não 26, já que não há menção de exclusão, não repetição ou algo assim.
Obrigada e bom fim de semana pra vcs!
Já comi 2 caixas de BIS azul pensando em como resolver esta questão!! rsss
= 343
, mas a resposta correta é 
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.