 por my2009 » Qui Ago 05, 2010 12:38
por my2009 » Qui Ago 05, 2010 12:38
Olá pessoal, tudo bem ? Depois de algum tempo de férias estou de volta = ] .
UMA EMPRESA IRÁ DIVIDIR R$ 24.000,00 ENTRE 4 FUNCIONARIOS DE FORMA DIRETAMENTE PROPORCIONAL AO TEMPO DE TRABALAHO NA EMPRESA E INVERSAMENTE PROPORCIONAL AO NÚMERO DE FALTAS MAIS UM.QUANTO COUBE AO FUNCIONÁRIO MAIS ANTIGO,SABENDO QUE MARCOS TRABALHA HÁ 6 ANOS NA EMPRESA E FALTOU 2 VEZES,AURÉLIO TRABALHA 2 ANOS E NUNCA FALTOU,JOEL TRABALHA HÁ 12 ANOS E FALTOU 3 VEZES E DANIEL TRABALHA HÁ 10 ANOS E FALTOU APENAS UMA VEZ ?
eu resolvi esse problema da seguinte forma :
M + A+ J+ D = 24.000
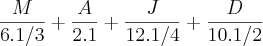
--- >

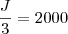
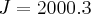

Existe outra forma para resolver esse problema ??? desde já agradeço xD
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por my2009 » Sex Ago 06, 2010 14:00
por my2009 » Sex Ago 06, 2010 14:00
Alguem pode me ajudar???
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por my2009 » Seg Ago 09, 2010 19:28
por my2009 » Seg Ago 09, 2010 19:28
Pessoal... preciso da resolução mas de outra forma, ninguem sabe ?

-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Sex Ago 20, 2010 13:39
por Cleyson007 » Sex Ago 20, 2010 13:39
Olá My, boa tarde!
A resolução que você apresentou está correta! Esse tipo de problema é resolvido dessa forma mesmo.
Valor de Marcos -->

(Onde 6 corresponde ao tempo de serviço e 3 corresponde ao n° de faltas + 1)
Logo,
M = R$ 4.000,00 Valor de Joel -->
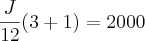
Logo,
J = R$ 6.000,00 (Funcionário mais antigo)
Valor de Aurélio -->

Logo,
A = R$ 4.000,00Valor de Daniel -->
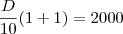
Logo,
D = R$ 10.000,00Espero ter ajudado!
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Prove usando a Propriedade Arquimediana...] Propriedade Arq
por alessandro » Seg Abr 16, 2012 19:10
- 1 Respostas
- 1661 Exibições
- Última mensagem por alessandro

Seg Abr 16, 2012 19:12
Sequências
-
- Somas
 por silvanuno11 » Seg Mar 26, 2012 20:38
por silvanuno11 » Seg Mar 26, 2012 20:38
- 1 Respostas
- 2697 Exibições
- Última mensagem por Guill

Dom Mai 27, 2012 22:28
Binômio de Newton
-
- Somas de Riemann
por andrerodrigues98 » Ter Dez 01, 2015 21:14
- 0 Respostas
- 1247 Exibições
- Última mensagem por andrerodrigues98

Ter Dez 01, 2015 21:14
Cálculo: Limites, Derivadas e Integrais
-
- Preço de venda com muitas somas de percentual
por SidneiSilveira » Sáb Mai 31, 2014 12:59
- 0 Respostas
- 2275 Exibições
- Última mensagem por SidneiSilveira

Sáb Mai 31, 2014 12:59
Matemática Financeira
-
- Demonstre a propriedade
por Aliocha Karamazov » Sáb Jul 09, 2011 02:02
- 1 Respostas
- 1342 Exibições
- Última mensagem por Guill

Dom Jul 10, 2011 09:33
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
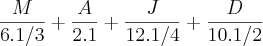 --- >
--- >
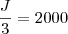
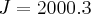




 (Onde 6 corresponde ao tempo de serviço e 3 corresponde ao n° de faltas + 1)
(Onde 6 corresponde ao tempo de serviço e 3 corresponde ao n° de faltas + 1)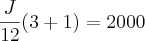

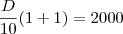

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.