Olá!
A questão diz: " Se a é uma raiz do polinômio p(x) e b é uma raiz do polinômio q(x), então:
a)p(b)/q(a) =1
b) p(a).q(b) =1
c) p(a)+q(b) =1
d) p(b).q(a) =0
e) p(a)+q(b)=0
Bom, a sendo raiz de p, o polinômio é divisível por a. Da mesma forma b. Então, não seria alternativa B, pois sendo divisível, o produto delas resultaria em 1??? Como desenvolvo uma relação entre as raízes e os polinômios?
Obrigada pela ajuda, Abraços!!!
e 
. Assim, as raízes serão respectivamente 
e 
, que farão o papel de 
e 
. O que você pode concluir com isso?
e 
, então 
e 
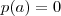é raíz de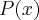 
e 
é raíz de 
, então 
e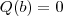 
. Vamos analisar as alternativas:
e nem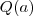 
, logo não podemos afirmar que 
.
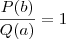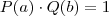é falso, pois ambos são zero.
.
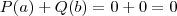![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)