três empresas X, Y e Z estão competindo, usando uma campanha de marketing. Como resultado desta campanha, houve a seguinte mudança de clientes:
- 7% dos clientes de X trocaram para Y
-> 5% dos clientes de X trocaram para Z
-> 14% dos clientes de Y trocaram para X
-> 8% dos clientes de Y trocam para Z
-> 3% dos clientes de Z trocaram para X
-> 5% dos clientes de Z trocaram para Y
Se no início da campanha a distribuição de clientes era
-> 39% para x
-> 26% para Y
-> 35% para Z
Que operação matricial pode ser usada para representar o cálculo da distribuição de clientes após o fim da campanha ?
A.
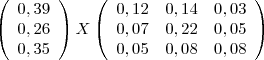
B.
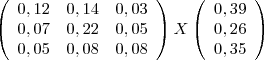
C.
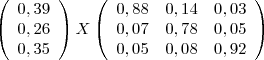
D.
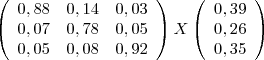
a alternativa C e A pode-se eliminar de imediato já que não podem multiplicar matriz
![[3X1][3X3]](/latexrender/pictures/5052052a0e5c36553fcaf66c8a8ae3f4.png "[3X1][3X3]")
estão não são permitem ser multiplicadas, restando as alternativas B e Dcheguei nos valores
x= 44%
Y = 16%
Z = 40%
fiz a multiplicação da matriz e o resultado não coincidiu
poderia verificar o que estou errando
fazendo a D que pelo gabarito é a correta não fecho como mostro abaixo
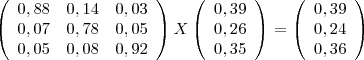
desde já agradeço a todos
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.