 por Jonatan » Qui Jul 08, 2010 01:47
por Jonatan » Qui Jul 08, 2010 01:47
Considere a função real f definida por:
f(x) =

- 1, se x < -2
f(x) =

, se
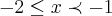
f(x) =

, se -1 < x < 1
f(x) =

, se 1 < x < 2
f(x) =

, se
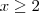
f(x) = 1, se x = 1
f(x) = 1, se x = -1
Determine o conjunto imagem da função.
Gabarito:
![] -\infty,-6] \cup {1} \cup [2, +\infty[ ] -\infty,-6] \cup {1} \cup [2, +\infty[](/latexrender/pictures/44a4de4fd84f9a9bed727a7e23300146.png)
-
Jonatan
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Jun 16, 2010 13:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Tom » Qui Jul 08, 2010 02:39
por Tom » Qui Jul 08, 2010 02:39
Vamos determinar a imagem de cada definição para a função e por fim fazer a união das imagens, conforme abaixo:
Para

, se
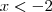
Temos
![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
Para
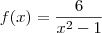
, se
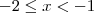
Temos
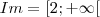
f(x) =

, se -1 < x < 1
Temos
![Im=]-\infty;-6] Im=]-\infty;-6]](/latexrender/pictures/d154951f49fb965459887579b8bc6ac8.png)
f(x) =

, se 1 < x < 2
Temos
![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
f(x) =

, se
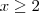
, temos
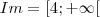
f(x) = 1, se x = 1 ,

f(x) = 1, se x = -1,

O conjunto imagem da função será:
![] -\infty,-6[ \cup {1} \cup [2, +\infty[ ] -\infty,-6[ \cup {1} \cup [2, +\infty[](/latexrender/pictures/a3655cd54b354b1f1fba6165180733fb.png)
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por Jonatan » Qui Jul 08, 2010 12:09
por Jonatan » Qui Jul 08, 2010 12:09
Ok, Tom. Mas para achar a imagem de uma lei de função dada eu devo atribuir valores para x que estão dentro do meu domínio para pode obter imagens y, correto? Mas no caso dessa questão, como faço para achar os valores que devo atribuir a x, uma vez que o domínio é real...
Pensei por exemplo na primeira lei que diz:
f(x) =

- 1 se x < -2
para x um valor real a meu critério valendo menos que -2:
x = -3
y =

- 1 = 8
É a partir daí que eu já não sei resolver o exercício, que, apesar de longo, não me parece ser difícil...
-
Jonatan
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Jun 16, 2010 13:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Tom » Qui Jul 08, 2010 12:58
por Tom » Qui Jul 08, 2010 12:58
A uma linguaguem formal, o que você deve ver são os limites que

assume, quando você faz

tender aos valores pré-definidos no domínio; respeitando sempre o comportamento assintótico das curvas.
Por exemplo, na primeira função, fazendo

tender a

, observamos que

tende a

e nota-se que para valroes menores que

, a função é estritamente crescente. Nao basta pegar valores intermediários no intervalo, mas sim os valores limitantes.
O que você deve fazer é analisar cada função passo a passo... Como em todos os casos aparece uma função do segundo grau, a imagem sempre está relacionada com o

Veja :
Para

, se
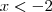
Imagine essa função com domínio no subconjunto real
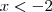
. Como se trata de uma função do segundo grau, de concavidade voltada para cima, a imagem irá de
![]y_v;+\infty[ ]y_v;+\infty[](/latexrender/pictures/4c6fdadaa68570acb13ceb44da625130.png)
ou do ponto de ordenada mais próximo do

e que tenha abicissa pertencente ao conjunto domínio dessa função particular.
Aplicando a relação do

, temos:
![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
Para esses três casos, é imediato obter o conjunto imagem.
f(x) =

, se
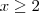
, temos
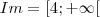
f(x) = 1, se x = 1 ,

f(x) = 1, se x = -1,

Para os demais casos:
Para
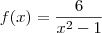
Novamente entenda que o dominio dessa função não é o conjunto real, mas sim os intervalos definidos em cada lei particular.
Perceba que o numerador é constante, então

depende do denominador, assim o quociente tem sempre o mesmo sinal do denominador.
Fazendo o estudo do sinal do denominador, isto é,
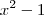
, observamos que:
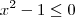
se
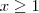
ou

e nesses casos a função tem um valor mínimo e cresce até

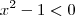
se
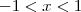
, e nesse caso a funçao apresenta valor minimo quando

o que decorre na imagem ser de

Decorre então que:
Para
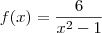
, se
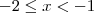
Temos
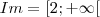
f(x) =

, se -1 < x < 1
Temos
![Im=]-\infty;-6] Im=]-\infty;-6]](/latexrender/pictures/d154951f49fb965459887579b8bc6ac8.png)
f(x) =

, se 1 < x < 2
Temos
![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
O conjunto imagem da função,como já falei, é a união dos intervalos anteriores e será:
![] -\infty,-6[ \cup {1} \cup [2, +\infty[ ] -\infty,-6[ \cup {1} \cup [2, +\infty[](/latexrender/pictures/a3655cd54b354b1f1fba6165180733fb.png)
Veja que a função

realmente tem domínio no conjunto real, já que se fizermos a união de todos os "domínios" das subfunções obtemos o conjunto real, de fato. O que ocorre é que

foi definida através de uma composição de leis.
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Conjunto imagem
por manuoliveira » Dom Jun 20, 2010 22:08
- 1 Respostas
- 2855 Exibições
- Última mensagem por Molina

Qua Jun 23, 2010 21:12
Trigonometria
-
- Conjunto imagem
por leosniper » Ter Mai 08, 2012 18:11
- 1 Respostas
- 1263 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 12, 2012 14:42
Trigonometria
-
- [Integral Dupla] Imagem do conjunto S - Mudança de Variável
por neymeirelles » Qua Mai 23, 2012 21:14
- 2 Respostas
- 2685 Exibições
- Última mensagem por neymeirelles

Sex Mai 25, 2012 12:18
Cálculo: Limites, Derivadas e Integrais
-
- Conjunto vazio está dentro de outro conjunto vazio?
por JDomingos » Dom Jul 20, 2014 07:41
- 1 Respostas
- 2231 Exibições
- Última mensagem por DanielFerreira

Dom Jul 20, 2014 12:14
Conjuntos
-
- Período e imagem
por David Soni » Qua Nov 25, 2009 10:33
- 1 Respostas
- 3204 Exibições
- Última mensagem por Molina

Qua Nov 25, 2009 14:28
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 - 1, se x < -2
- 1, se x < -2 , se
, se 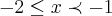
 , se -1 < x < 1
, se -1 < x < 1 , se 1 < x < 2
, se 1 < x < 2 , se
, se 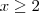
![] -\infty,-6] \cup {1} \cup [2, +\infty[ ] -\infty,-6] \cup {1} \cup [2, +\infty[](/latexrender/pictures/44a4de4fd84f9a9bed727a7e23300146.png)

 - 1, se x < -2
- 1, se x < -2 , se
, se 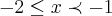
 , se -1 < x < 1
, se -1 < x < 1 , se 1 < x < 2
, se 1 < x < 2 , se
, se 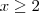
![] -\infty,-6] \cup {1} \cup [2, +\infty[ ] -\infty,-6] \cup {1} \cup [2, +\infty[](/latexrender/pictures/44a4de4fd84f9a9bed727a7e23300146.png)

 , se
, se 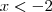
![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
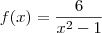 , se
, se 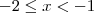
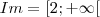
 , se -1 < x < 1
, se -1 < x < 1![Im=]-\infty;-6] Im=]-\infty;-6]](/latexrender/pictures/d154951f49fb965459887579b8bc6ac8.png)
 , se 1 < x < 2
, se 1 < x < 2![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
 , se
, se 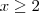 , temos
, temos 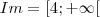


![] -\infty,-6[ \cup {1} \cup [2, +\infty[ ] -\infty,-6[ \cup {1} \cup [2, +\infty[](/latexrender/pictures/a3655cd54b354b1f1fba6165180733fb.png)

 - 1 se x < -2
- 1 se x < -2 - 1 = 8
- 1 = 8
 assume, quando você faz
assume, quando você faz  tender aos valores pré-definidos no domínio; respeitando sempre o comportamento assintótico das curvas.
tender aos valores pré-definidos no domínio; respeitando sempre o comportamento assintótico das curvas. tender a
tender a  , observamos que
, observamos que  tende a
tende a  e nota-se que para valroes menores que
e nota-se que para valroes menores que  , a função é estritamente crescente. Nao basta pegar valores intermediários no intervalo, mas sim os valores limitantes.
, a função é estritamente crescente. Nao basta pegar valores intermediários no intervalo, mas sim os valores limitantes.
 , se
, se 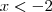
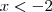 . Como se trata de uma função do segundo grau, de concavidade voltada para cima, a imagem irá de
. Como se trata de uma função do segundo grau, de concavidade voltada para cima, a imagem irá de ![]y_v;+\infty[ ]y_v;+\infty[](/latexrender/pictures/4c6fdadaa68570acb13ceb44da625130.png) ou do ponto de ordenada mais próximo do
ou do ponto de ordenada mais próximo do  e que tenha abicissa pertencente ao conjunto domínio dessa função particular.
e que tenha abicissa pertencente ao conjunto domínio dessa função particular. , temos:
, temos: ![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
 , se
, se 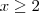 , temos
, temos 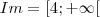


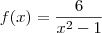
 depende do denominador, assim o quociente tem sempre o mesmo sinal do denominador.
depende do denominador, assim o quociente tem sempre o mesmo sinal do denominador.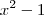 , observamos que:
, observamos que: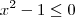 se
se 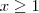 ou
ou  e nesses casos a função tem um valor mínimo e cresce até
e nesses casos a função tem um valor mínimo e cresce até 
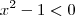 se
se 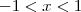 , e nesse caso a funçao apresenta valor minimo quando
, e nesse caso a funçao apresenta valor minimo quando  o que decorre na imagem ser de
o que decorre na imagem ser de 
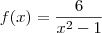 , se
, se 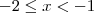
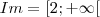
 , se -1 < x < 1
, se -1 < x < 1![Im=]-\infty;-6] Im=]-\infty;-6]](/latexrender/pictures/d154951f49fb965459887579b8bc6ac8.png)
 , se 1 < x < 2
, se 1 < x < 2![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
![] -\infty,-6[ \cup {1} \cup [2, +\infty[ ] -\infty,-6[ \cup {1} \cup [2, +\infty[](/latexrender/pictures/a3655cd54b354b1f1fba6165180733fb.png)
 realmente tem domínio no conjunto real, já que se fizermos a união de todos os "domínios" das subfunções obtemos o conjunto real, de fato. O que ocorre é que
realmente tem domínio no conjunto real, já que se fizermos a união de todos os "domínios" das subfunções obtemos o conjunto real, de fato. O que ocorre é que  foi definida através de uma composição de leis.
foi definida através de uma composição de leis.
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?