f(x) =
 - 1, se x < -2
- 1, se x < -2f(x) =
 , se
, se 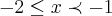
f(x) =
 , se -1 < x < 1
, se -1 < x < 1f(x) =
 , se 1 < x < 2
, se 1 < x < 2f(x) =
 , se
, se 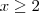
f(x) = 1, se x = 1
f(x) = 1, se x = -1
Determine o conjunto imagem da função.
Gabarito:
![] -\infty,-6] \cup {1} \cup [2, +\infty[ ] -\infty,-6] \cup {1} \cup [2, +\infty[](/latexrender/pictures/44a4de4fd84f9a9bed727a7e23300146.png)

 - 1, se x < -2
- 1, se x < -2 , se
, se 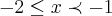
 , se -1 < x < 1
, se -1 < x < 1 , se 1 < x < 2
, se 1 < x < 2 , se
, se 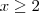
![] -\infty,-6] \cup {1} \cup [2, +\infty[ ] -\infty,-6] \cup {1} \cup [2, +\infty[](/latexrender/pictures/44a4de4fd84f9a9bed727a7e23300146.png)

 , se
, se 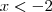
![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
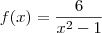 , se
, se 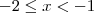
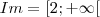
 , se -1 < x < 1
, se -1 < x < 1![Im=]-\infty;-6] Im=]-\infty;-6]](/latexrender/pictures/d154951f49fb965459887579b8bc6ac8.png)
 , se 1 < x < 2
, se 1 < x < 2![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
 , se
, se 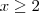 , temos
, temos 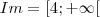


![] -\infty,-6[ \cup {1} \cup [2, +\infty[ ] -\infty,-6[ \cup {1} \cup [2, +\infty[](/latexrender/pictures/a3655cd54b354b1f1fba6165180733fb.png)

 - 1 se x < -2
- 1 se x < -2 - 1 = 8
- 1 = 8
 assume, quando você faz
assume, quando você faz  tender aos valores pré-definidos no domínio; respeitando sempre o comportamento assintótico das curvas.
tender aos valores pré-definidos no domínio; respeitando sempre o comportamento assintótico das curvas. tender a
tender a  , observamos que
, observamos que  tende a
tende a  e nota-se que para valroes menores que
e nota-se que para valroes menores que  , a função é estritamente crescente. Nao basta pegar valores intermediários no intervalo, mas sim os valores limitantes.
, a função é estritamente crescente. Nao basta pegar valores intermediários no intervalo, mas sim os valores limitantes.
 , se
, se 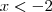
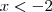 . Como se trata de uma função do segundo grau, de concavidade voltada para cima, a imagem irá de
. Como se trata de uma função do segundo grau, de concavidade voltada para cima, a imagem irá de ![]y_v;+\infty[ ]y_v;+\infty[](/latexrender/pictures/4c6fdadaa68570acb13ceb44da625130.png) ou do ponto de ordenada mais próximo do
ou do ponto de ordenada mais próximo do  e que tenha abicissa pertencente ao conjunto domínio dessa função particular.
e que tenha abicissa pertencente ao conjunto domínio dessa função particular. , temos:
, temos: ![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
 , se
, se 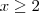 , temos
, temos 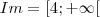


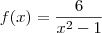
 depende do denominador, assim o quociente tem sempre o mesmo sinal do denominador.
depende do denominador, assim o quociente tem sempre o mesmo sinal do denominador.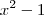 , observamos que:
, observamos que: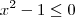 se
se 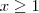 ou
ou  e nesses casos a função tem um valor mínimo e cresce até
e nesses casos a função tem um valor mínimo e cresce até 
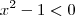 se
se 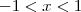 , e nesse caso a funçao apresenta valor minimo quando
, e nesse caso a funçao apresenta valor minimo quando  o que decorre na imagem ser de
o que decorre na imagem ser de 
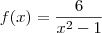 , se
, se 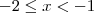
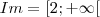
 , se -1 < x < 1
, se -1 < x < 1![Im=]-\infty;-6] Im=]-\infty;-6]](/latexrender/pictures/d154951f49fb965459887579b8bc6ac8.png)
 , se 1 < x < 2
, se 1 < x < 2![Im=]3;+\infty[ Im=]3;+\infty[](/latexrender/pictures/e80868f8adb082d9cf133bbe183d345f.png)
![] -\infty,-6[ \cup {1} \cup [2, +\infty[ ] -\infty,-6[ \cup {1} \cup [2, +\infty[](/latexrender/pictures/a3655cd54b354b1f1fba6165180733fb.png)
 realmente tem domínio no conjunto real, já que se fizermos a união de todos os "domínios" das subfunções obtemos o conjunto real, de fato. O que ocorre é que
realmente tem domínio no conjunto real, já que se fizermos a união de todos os "domínios" das subfunções obtemos o conjunto real, de fato. O que ocorre é que  foi definida através de uma composição de leis.
foi definida através de uma composição de leis.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

