 por Fernanda Lauton » Sáb Jul 03, 2010 22:53
por Fernanda Lauton » Sáb Jul 03, 2010 22:53
Em:
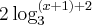
a única razão de ser do parêntesis em (x + 1) é porque só ele estaria elavado a dois

tipo:

será que estou certa

Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por vyhonda » Sáb Jul 03, 2010 23:10
por vyhonda » Sáb Jul 03, 2010 23:10
Caso o (x+1)+2 for o Logaritmando, então todo o logaritmando será elevado a 2ª potência ex: [(x+1)+2]²;
Sua afirmação estaria correta caso o
+2 não fosse o logaritmando,
então ficaria :
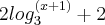
=>

-
vyhonda
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Jan 17, 2010 20:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Materiais - Unesp
- Andamento: cursando
 por Fernanda Lauton » Dom Jul 04, 2010 17:21
por Fernanda Lauton » Dom Jul 04, 2010 17:21
Tá, mas então para que serve este parêntese

porque a expressão não é escrita sem ele

Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por MarceloFantini » Seg Jul 05, 2010 00:51
por MarceloFantini » Seg Jul 05, 2010 00:51
Porque

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Fernanda Lauton » Seg Jul 05, 2010 13:37
por Fernanda Lauton » Seg Jul 05, 2010 13:37
Ah sim, prefeitamente

muito obrigada aos dois ^^

Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Funções] Pequena dúvida
por Renato_RJ » Sex Jan 13, 2012 19:44
- 4 Respostas
- 2572 Exibições
- Última mensagem por Renato_RJ

Sáb Jan 14, 2012 18:06
Funções
-
- Potência - Pequena dúvida
por CaioCaesar » Seg Abr 16, 2012 07:14
- 1 Respostas
- 1433 Exibições
- Última mensagem por jacobi

Qua Abr 18, 2012 10:43
Álgebra Elementar
-
- sistema de equações do 2º grau pequena dúvida
por TAE » Sex Jun 08, 2012 20:24
- 1 Respostas
- 2023 Exibições
- Última mensagem por Molina

Sáb Jun 09, 2012 14:37
Sistemas de Equações
-
- Tamanho da amostra - população heterogenia e pequena
por Roniberto » Sex Fev 13, 2009 15:41
- 2 Respostas
- 2873 Exibições
- Última mensagem por Roniberto

Ter Fev 17, 2009 09:22
Estatística
-
- Pequena ajuda de "arranque"!
por eicma » Sex Dez 11, 2009 14:29
- 0 Respostas
- 991 Exibições
- Última mensagem por eicma

Sex Dez 11, 2009 14:29
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
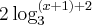 a única razão de ser do parêntesis em (x + 1) é porque só ele estaria elavado a dois
a única razão de ser do parêntesis em (x + 1) é porque só ele estaria elavado a dois  será que estou certa
será que estou certa 
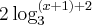 a única razão de ser do parêntesis em (x + 1) é porque só ele estaria elavado a dois
a única razão de ser do parêntesis em (x + 1) é porque só ele estaria elavado a dois  será que estou certa
será que estou certa 
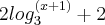 =>
=> 



