Sabendo que a função f é contínua em |R e:



qual será a expressão de f que satisfaz as condições acima?
Já substitui o x por 1, mas nenhuma função me dá o pi....e não vejo outra forma de descobrir a função! (será que tenho de igualar uma expressão por pi?)
Agradecia muito uma ajuda da vossa parte


 .
.

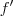 é definida por duas leis mediante o intervalo do conjunto domínio, então
é definida por duas leis mediante o intervalo do conjunto domínio, então  também o será. Assim:
também o será. Assim: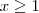 :
: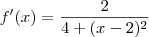
![f=\int\frac{2}{4+(x-2)^{2}}=\int\dfrac{2}{4}\times\dfrac{1}{1+(\frac{x-2}{2})^2}=\frac{1}{2}\int\frac{1}{1+(\frac{x-2}{2})^2}=\frac{1}{2}\int\frac{2[\frac{x-2}{2}]'}{1+(\frac{x-2}{2})^2}= f=\int\frac{2}{4+(x-2)^{2}}=\int\dfrac{2}{4}\times\dfrac{1}{1+(\frac{x-2}{2})^2}=\frac{1}{2}\int\frac{1}{1+(\frac{x-2}{2})^2}=\frac{1}{2}\int\frac{2[\frac{x-2}{2}]'}{1+(\frac{x-2}{2})^2}=](/latexrender/pictures/1625f9bcfd807a4c2daf6ed5cdc19b8a.png)
![\int\frac{[\frac{x-2}{2}]'}{1+(\frac{x-2}{2})^2}=arctg(\frac{x-2}{2})+C_1 \int\frac{[\frac{x-2}{2}]'}{1+(\frac{x-2}{2})^2}=arctg(\frac{x-2}{2})+C_1](/latexrender/pictures/492b99e0b4fb3f919e2c000ed0fca8ef.png)
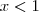 :
:

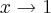 devem ser iguais. Então:
devem ser iguais. Então:
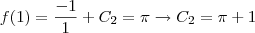
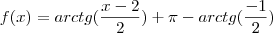 , se
, se 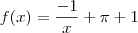 , se
, se 

 .
.
 :
: