 por hevhoram » Seg Jun 21, 2010 13:19
por hevhoram » Seg Jun 21, 2010 13:19
ola pessoal fiquei em duvida numa questao de um concurso
é o seguinte:
sabemos que o cociente de dois numeros irracionais pode ser um numero racional. Das alternativas abaixo, qual exemplifica essa afirmação?
a)
![\frac{\sqrt[]{2}}{\sqrt[]{4}} \frac{\sqrt[]{2}}{\sqrt[]{4}}](/latexrender/pictures/7164a9a9b857fd1c37bc40472aa70b46.png)
=
![\frac{1}{\sqrt[]{2}} \frac{1}{\sqrt[]{2}}](/latexrender/pictures/a708a9a9173a86197e94e74a716f2bea.png)
b)
![\frac{\sqrt[]{2}}{\sqrt[]{18}} \frac{\sqrt[]{2}}{\sqrt[]{18}}](/latexrender/pictures/dfa194d9e2fe78cf1c7d6984df16a7bd.png)
=
![\frac{1}{\sqrt[]{9}} \frac{1}{\sqrt[]{9}}](/latexrender/pictures/b3db8d58f558413c5f5cafa466991c47.png)
porque a letra a nao vai resultar tambem num numero racional???
fiz meios por extremos e as duas alternativas deu 1 porque a letra a nao é racional
Editado pela última vez por
hevhoram em Seg Jun 21, 2010 13:29, em um total de 1 vez.
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por hevhoram » Seg Jun 21, 2010 13:21
por hevhoram » Seg Jun 21, 2010 13:21
pis fiz meios por extremos e os dois deram o numero 1 ??? porque a letra a nao é ???
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por MarceloFantini » Qui Jun 24, 2010 08:25
por MarceloFantini » Qui Jun 24, 2010 08:25
Porque
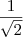
não é racional. Já

, logo racional.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por hevhoram » Qui Jun 24, 2010 11:35
por hevhoram » Qui Jun 24, 2010 11:35
mas fazendo meios por extremos a raiz de 2 vezes raiz de 2 nao dá raiz de quatro que é igual a 2. nao é pelo metodo de meios por extremos??? nao entendi???
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por MarceloFantini » Qui Jun 24, 2010 14:05
por MarceloFantini » Qui Jun 24, 2010 14:05
O que é esse método dos meios pelos extremos?
Em tempo:

Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gustavowelp » Sáb Jun 26, 2010 02:37
por gustavowelp » Sáb Jun 26, 2010 02:37
Sem querer me intrometer, por que
![\sqrt[2]{2} / \sqrt[2]{18} = 1 / \sqrt[2]{9} \sqrt[2]{2} / \sqrt[2]{18} = 1 / \sqrt[2]{9}](/latexrender/pictures/028f397ba376a7e42a7fa60b210bf989.png)
?
Sei que deve ser questão básica, e deu certo usando calculadora, mas não entendo matematicamente o porquê...
Obrigado
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- raiz para numero racional
por hevhoram » Seg Jun 21, 2010 13:26
- 1 Respostas
- 1087 Exibições
- Última mensagem por MarceloFantini

Ter Jun 22, 2010 00:53
Álgebra Elementar
-
- número:racional
por Victor Gabriel » Seg Jun 17, 2013 16:40
- 0 Respostas
- 1120 Exibições
- Última mensagem por Victor Gabriel

Seg Jun 17, 2013 16:40
Teoria dos Números
-
- Número Racional
por marinalcd » Ter Set 19, 2017 17:13
- 0 Respostas
- 1534 Exibições
- Última mensagem por marinalcd

Ter Set 19, 2017 17:13
Aritmética
-
- [Integral de fração racional] Deduza uma formiula para:
por Job1992 » Ter Nov 26, 2013 22:29
- 1 Respostas
- 1759 Exibições
- Última mensagem por e8group

Sáb Nov 30, 2013 21:27
Cálculo: Limites, Derivadas e Integrais
-
- Função Racional - preciso de ajuda para hoje ainda!
por raf » Seg Set 28, 2015 14:32
- 1 Respostas
- 2604 Exibições
- Última mensagem por nakagumahissao

Sex Out 02, 2015 00:47
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\sqrt[]{2}}{\sqrt[]{4}} \frac{\sqrt[]{2}}{\sqrt[]{4}}](/latexrender/pictures/7164a9a9b857fd1c37bc40472aa70b46.png) =
= ![\frac{1}{\sqrt[]{2}} \frac{1}{\sqrt[]{2}}](/latexrender/pictures/a708a9a9173a86197e94e74a716f2bea.png)
![\frac{\sqrt[]{2}}{\sqrt[]{18}} \frac{\sqrt[]{2}}{\sqrt[]{18}}](/latexrender/pictures/dfa194d9e2fe78cf1c7d6984df16a7bd.png) =
= ![\frac{1}{\sqrt[]{9}} \frac{1}{\sqrt[]{9}}](/latexrender/pictures/b3db8d58f558413c5f5cafa466991c47.png)


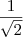 não é racional. Já
não é racional. Já  , logo racional.
, logo racional.


![\sqrt[2]{2} / \sqrt[2]{18} = 1 / \sqrt[2]{9} \sqrt[2]{2} / \sqrt[2]{18} = 1 / \sqrt[2]{9}](/latexrender/pictures/028f397ba376a7e42a7fa60b210bf989.png) ?
?





