Caros Colegas me ajudem nessa!
Tenho uma população de 761 elementos, a avariavel a ser estudada é idade, o exercicio pede uma amostra com nivel de confiança de 95% e erro de 4,5 anos. Acontece que quando aplico a formula para determinação da amostra para a média aritmetica, como a população é muito homogênea (o desvio padrão ficou em 4,93) a amostra calculada ficou em 5 elementos, muito pouco para fazer o restante de exercicio (divisão em 5 classes, frequencia) existe outra forma para definir uma amostra maior? Qual seria?
Por gentileza, socorram-me (rs)!!!
Abraços
Márcia
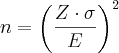
: número de indivíduos da amostra;
: valor crítico correspondente ao grau de confiança;
: desvio padrão populacional da variável estudada;
: margem de erro (diferença máxima entre a média amostral e a verdadeira média populacional).
elementos:
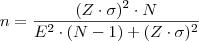
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.