Dúvidas pendentes de estatística ou outras áreas (física, química etc), aguardando bacharéis dispostos e habilitados a ajudar.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por marciabarbosa2 » Qui Jun 05, 2008 19:09
por marciabarbosa2 » Qui Jun 05, 2008 19:09
Caros Colegas me ajudem nessa!
Tenho uma população de 761 elementos, a avariavel a ser estudada é idade, o exercicio pede uma amostra com nivel de confiança de 95% e erro de 4,5 anos. Acontece que quando aplico a formula para determinação da amostra para a média aritmetica, como a população é muito homogênea (o desvio padrão ficou em 4,93) a amostra calculada ficou em 5 elementos, muito pouco para fazer o restante de exercicio (divisão em 5 classes, frequencia) existe outra forma para definir uma amostra maior? Qual seria?
Por gentileza, socorram-me (rs)!!!
Abraços
Márcia
-
marciabarbosa2
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Jun 05, 2008 18:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: enfermagem
- Andamento: cursando
 por admin » Qui Jun 05, 2008 22:57
por admin » Qui Jun 05, 2008 22:57
Olá Márcia, boa noite, seja bem-vinda!
Como eu não sou bacharel em estatística, assumo um posicionamento informal apenas como estudante curioso.
Pelo que vi, há uma distinção sim para o cálculo da amostragem, considerando se a população é "finita" ou "infinita", sendo estas "fórmulas" provenientes do Teorema do Limite Central (TLC).
Você está calculando assim?
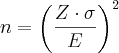
Onde:

: número de indivíduos da amostra;

: valor crítico correspondente ao grau de confiança;

: desvio padrão populacional da variável estudada;

: margem de erro (diferença máxima entre a média amostral e a verdadeira média populacional).
Com o fator de correção, considerando uma amostra finita com

elementos:
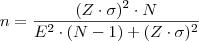
Mas, mesmo assim os valores obtidos para

ainda estão bem próximos.
O desvio padrão está correto?
Você está utilizando algum livro como referência bibliográfica?
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por marciabarbosa2 » Sex Jun 06, 2008 15:12
por marciabarbosa2 » Sex Jun 06, 2008 15:12
Obrigada Fábio!
Bom, estou usando o livro "Estatistica: Teoria e Aplicações - Usando Microsoft Excel em protugues" de David M. Levine, Mark L. Berenson. O desvio padrão calculei pela opção,`"analise de Dados - Estatistica Descritiva ( e deu 4,5
mesmo)...as fórmulas que utlizei foram essas mesma que vc citou para a definição da amostra finita, mas 5 é muito pouco!! Não sei mais o que faço e infelizmente não estou podendo recorrer ao professor!!!
De qualquer sorte, vamos ver se alguem ainda pode me ajudar!
Sds
Márcia Matos
-
marciabarbosa2
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Jun 05, 2008 18:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: enfermagem
- Andamento: cursando
 por admin » Sex Jun 06, 2008 17:59
por admin » Sex Jun 06, 2008 17:59
Olá Márcia, boa tarde.
Você tem a informação sobre a média da população?
Ou melhor, convém enviar o enunciado completo, se possível.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por marciabarbosa2 » Dom Jun 08, 2008 12:12
por marciabarbosa2 » Dom Jun 08, 2008 12:12
Enunciado:
População: 761 registros capturados do banco de efetivo da Empresa Y referentes ao mes de maio de 2008.
De posse dos dados apresentados obtidos faça um estudo amsotral, considerando as variáveis, "idade", devendo a atividade seguir o roteito na sua formulação:
Calcular o tamanho da amostra dentro da população como tamanho da amostra com erro de 4,5 anos de idade e nível de confiança de 95%.
Média aritmética: 44,63 ( Amplitudes: mínima da população 35 anos e máxima 60 anos).
-
marciabarbosa2
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Jun 05, 2008 18:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: enfermagem
- Andamento: cursando
 por professor9 » Qua Dez 02, 2009 23:11
por professor9 » Qua Dez 02, 2009 23:11
Gostaria de aprofundar mais sobre este assunto, ou seja, quais elementos preciso ter para aplicar a formula?
e como desnevolver esta formula no Excel?
-
professor9
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Dez 02, 2009 23:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: formado
Voltar para Dúvidas Pendentes (aguardando novos colaboradores)
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Urgente estatistica
por Wellington » Qua Jun 04, 2008 16:21
- 1 Respostas
- 2944 Exibições
- Última mensagem por admin

Qua Jun 04, 2008 17:20
Estatística
-
- URGENTE: PROBLEMA DE ESTATISTICA
 por robson2320 » Qui Jul 22, 2010 22:40
por robson2320 » Qui Jul 22, 2010 22:40
- 1 Respostas
- 3750 Exibições
- Última mensagem por Lucio Carvalho

Sex Jul 23, 2010 19:47
Estatística
-
- Estatística - Exercício Urgente
por Carlaipb » Qua Out 05, 2011 17:12
- 1 Respostas
- 2219 Exibições
- Última mensagem por Neperiano

Qua Out 19, 2011 18:52
Estatística
-
- análise estatistica - SPSS - Urgente
por eueu » Qui Jun 10, 2010 10:18
- 1 Respostas
- 2080 Exibições
- Última mensagem por Neperiano

Qua Out 05, 2011 17:59
Estatística
-
- [exercicio de estatistica basica] URGENTE POR FAVOR
por ddesrosiers » Sex Dez 09, 2016 00:31
- 0 Respostas
- 7620 Exibições
- Última mensagem por ddesrosiers

Sex Dez 09, 2016 00:31
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


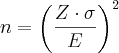
 : número de indivíduos da amostra;
: número de indivíduos da amostra; : valor crítico correspondente ao grau de confiança;
: valor crítico correspondente ao grau de confiança; : desvio padrão populacional da variável estudada;
: desvio padrão populacional da variável estudada; : margem de erro (diferença máxima entre a média amostral e a verdadeira média populacional).
: margem de erro (diferença máxima entre a média amostral e a verdadeira média populacional). elementos:
elementos: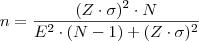



 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
