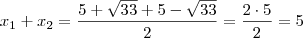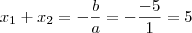Mais uma vez venha até aqui pedir ajuda. Abaixo está a expressão que eu devo resolver e a minha resolução!
->Seja a equação det(A-x.I)=0 onde A=
 , x
, x  R e I a matriz identidade.Determine a soma das raízes desta equação.
R e I a matriz identidade.Determine a soma das raízes desta equação.Então resolvi assim:
Primerio fiz a I.x e como a matriz A é de ordem 2 supus que a identidade também é, assim:
 . x =
. x = 
Depois subtraí com a matriz A:
 -
-  =
= 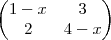
Calculando o determinante:
(1-x).(4-x) - 2.3=0
4 - x - 4x + x² - 6 = 0
x²-5x -2= 0
 - 4.1.(-2)
- 4.1.(-2)
x'=
![\frac{5+\sqrt[]{33}}2{} \frac{5+\sqrt[]{33}}2{}](/latexrender/pictures/428a0c751c0b9ee4f06e70d4898bb0ba.png)
x"=
![\frac{5-\sqrt[]{33}}2{} \frac{5-\sqrt[]{33}}2{}](/latexrender/pictures/246318cf76a76d78512929b1e2537a83.png)
Esses foram os meus resultados, cujo o resultado da soma deveria ser igual a 5
Não sei o que eu resolvi errado, alguém me ajuda?
Muito Obrigadaaaa mais uma vez!