 por Bruhh » Sáb Jun 05, 2010 18:59
por Bruhh » Sáb Jun 05, 2010 18:59
Olá a todos

Mais uma vez venha até aqui pedir ajuda. Abaixo está a expressão que eu devo resolver e a minha resolução!
->Seja a equação det(A-x.I)=0 onde A=

, x

R e I a matriz identidade.Determine a soma das raízes desta equação.
Então resolvi assim:
Primerio fiz a I.x e como a matriz A é de ordem 2 supus que a identidade também é, assim:

. x =

Depois subtraí com a matriz A:

-

=
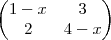
Calculando o determinante:
(1-x).(4-x) - 2.3=0
4 - x - 4x + x² - 6 = 0
x²-5x -2= 0

- 4.1.(-2)

x'=
![\frac{5+\sqrt[]{33}}2{} \frac{5+\sqrt[]{33}}2{}](/latexrender/pictures/428a0c751c0b9ee4f06e70d4898bb0ba.png)
x"=
![\frac{5-\sqrt[]{33}}2{} \frac{5-\sqrt[]{33}}2{}](/latexrender/pictures/246318cf76a76d78512929b1e2537a83.png)
Esses foram os meus resultados, cujo o resultado da soma deveria ser igual a 5
Não sei o que eu resolvi errado, alguém me ajuda?
Muito Obrigadaaaa mais uma vez!
-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
 por Bruhh » Dom Jun 06, 2010 14:34
por Bruhh » Dom Jun 06, 2010 14:34
Nossa, juro para você, que fiz o cálculo inteiro na calculadora científica e ela me deu como resultado 7,.......!Hehehe
Mas de toda forma, muito obrigada!

-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ITA) Calcular x + y
por Carolziiinhaaah » Qui Jun 24, 2010 14:47
- 3 Respostas
- 2636 Exibições
- Última mensagem por DanielFerreira

Ter Jun 29, 2010 16:37
Matrizes e Determinantes
-
- calcular:
por willwgo » Qui Mai 05, 2011 16:33
- 1 Respostas
- 1629 Exibições
- Última mensagem por FilipeCaceres

Qui Mai 05, 2011 19:51
Polinômios
-
- Calcular a.b
por -civil- » Ter Set 20, 2011 23:29
- 3 Respostas
- 2612 Exibições
- Última mensagem por MarceloFantini

Qui Set 29, 2011 21:07
Polinômios
-
- (Calcular)
por Veronica Souza » Ter Abr 24, 2012 13:06
- 6 Respostas
- 4308 Exibições
- Última mensagem por Fabiano Vieira

Seg Mai 28, 2012 23:30
Matemática Financeira
-
- [calcular f(6) ]
por JKS » Sáb Jun 29, 2013 03:33
- 1 Respostas
- 2335 Exibições
- Última mensagem por nakagumahissao

Qua Out 07, 2015 21:10
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 , x
, x  R e I a matriz identidade.Determine a soma das raízes desta equação.
R e I a matriz identidade.Determine a soma das raízes desta equação. . x =
. x = 
 -
-  =
= 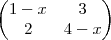
 - 4.1.(-2)
- 4.1.(-2)
![\frac{5+\sqrt[]{33}}2{} \frac{5+\sqrt[]{33}}2{}](/latexrender/pictures/428a0c751c0b9ee4f06e70d4898bb0ba.png)
![\frac{5-\sqrt[]{33}}2{} \frac{5-\sqrt[]{33}}2{}](/latexrender/pictures/246318cf76a76d78512929b1e2537a83.png)


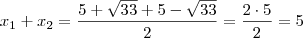



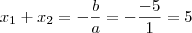
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.