1) Sendo
 e
e  , determine:
, determine:a)
![f[g(x)] f[g(x)]](/latexrender/pictures/2b71afbb39434a94a1dbee0d85b8ba83.png)
b)
![g[f(x)] g[f(x)]](/latexrender/pictures/b6b256ffe0a66f87c821c68b1e67258e.png)
Se puder fazer passo a passo para que eu consiga mesmo aprender agradeço
Não sei pq está aparecendo esse A grande, ele não existe é x ao quadrado apenas

 e
e  , determine:
, determine:![f[g(x)] f[g(x)]](/latexrender/pictures/2b71afbb39434a94a1dbee0d85b8ba83.png)
![g[f(x)] g[f(x)]](/latexrender/pictures/b6b256ffe0a66f87c821c68b1e67258e.png)





DaniellaFlavia escreveu:Não consegui, vc pode me ajudar no passo a passo E obrigado pela explicação do LaTeX.
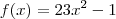 e
e 
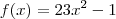 (f de x)
(f de x)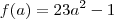 (f de a)
(f de a)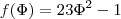 (f de phi)
(f de phi) (f de bolinha)
(f de bolinha)![f[g(x)] f[g(x)]](/latexrender/pictures/2b71afbb39434a94a1dbee0d85b8ba83.png)
![f[g(x)]=23g(x)^2-1 f[g(x)]=23g(x)^2-1](/latexrender/pictures/bdb8dd951a9a3fb01e5829fb1a3dbea1.png) (f de g(x))
(f de g(x))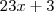 :
:![f[g(x)]=23g(x)^2-1 f[g(x)]=23g(x)^2-1](/latexrender/pictures/bdb8dd951a9a3fb01e5829fb1a3dbea1.png)
![f[g(x)]=23*(23x+3)^2-1 f[g(x)]=23*(23x+3)^2-1](/latexrender/pictures/1d5af4d5c6f75a9f6e0c7fefb173fd87.png)
![f[g(x)]=23*(529x^2+138x+9)-1 f[g(x)]=23*(529x^2+138x+9)-1](/latexrender/pictures/342a7aada6ea9a40b611f46ff4c78660.png)
![f[g(x)]=12167x^2+3174x+206 f[g(x)]=12167x^2+3174x+206](/latexrender/pictures/dc31ae7e1a9784f8830f334e6c073d43.png)



 pelo valor de
pelo valor de  ?
?
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes