 por DaniellaFlavia » Dom Mai 30, 2010 14:02
por DaniellaFlavia » Dom Mai 30, 2010 14:02
Estou com dificuldade em funções, sempre fui boa aluna mas agora sei lá... A sala toda está com dificuldade achamos que é o professor mas ele diz que não e ai fico na mesma não sei a matéria. Como não quero levar bomba me ajudem.
1) Sendo

e

, determine:
a)
![f[g(x)] f[g(x)]](/latexrender/pictures/2b71afbb39434a94a1dbee0d85b8ba83.png)
b)
![g[f(x)] g[f(x)]](/latexrender/pictures/b6b256ffe0a66f87c821c68b1e67258e.png)
Se puder fazer passo a passo para que eu consiga mesmo aprender agradeço
Não sei pq está aparecendo esse A grande, ele não existe é x ao quadrado apenas
Editado pela última vez por
DaniellaFlavia em Dom Mai 30, 2010 14:18, em um total de 1 vez.
-
DaniellaFlavia
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Mai 30, 2010 13:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Neperiano » Dom Mai 30, 2010 14:05
por Neperiano » Dom Mai 30, 2010 14:05
Ola
Na a voce deve copiar a função f e substituir o x pelo valor de g(x), ou seja:
23(23x+3)A^2-1
Olha eu não sei o que é o A grande por isso não poderei ajudar na resolução
Na b ao contrario
23(23xA^2-1)+3
Primeiro resolva os parenteses e multiplique
Espero ter ajudado
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por DaniellaFlavia » Dom Mai 30, 2010 14:36
por DaniellaFlavia » Dom Mai 30, 2010 14:36
Não sei pq está aparecendo aquele A grande, mas é apenas x ao quadrado.
Obrigado pela força
-
DaniellaFlavia
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Mai 30, 2010 13:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Dom Mai 30, 2010 14:46
por Molina » Dom Mai 30, 2010 14:46
Arrumei essa questão do "A grande".
Aparece esse "A" por causa do uso do LaTeX. Quando você usar [tex] e [/tex], você não pode usar o ², senão aparece aquele "A".
Modo que você escreveu: [tex]f(x)=23.x²-1[/tex] (modo errado)
Modo que tem que ser escrito: [tex]f(x)=23.x^2-1[/tex] (modo correto)
Qualquer dúvida quanto a digitação do LaTeX me procure!
E sobre a questão, conseguiu entender como resolvê-la?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por DaniellaFlavia » Dom Mai 30, 2010 14:50
por DaniellaFlavia » Dom Mai 30, 2010 14:50
Não consegui, vc pode me ajudar no passo a passo E obrigado pela explicação do LaTeX.
-
DaniellaFlavia
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Mai 30, 2010 13:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Dom Mai 30, 2010 15:19
por Molina » Dom Mai 30, 2010 15:19
DaniellaFlavia escreveu:Não consegui, vc pode me ajudar no passo a passo E obrigado pela explicação do LaTeX.
Ok, Daniella.
Você tem duas funções:
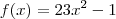
e

Numa função, tudo que tiver dentro do parênteses de f(_) nós substituiremos na função. Por exemplo:
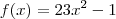 (f de x)
(f de x)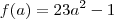 (f de a)
(f de a)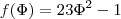 (f de phi)
(f de phi) (f de bolinha)
(f de bolinha).
.
.
E assim por diante.
a)
![f[g(x)] f[g(x)]](/latexrender/pictures/2b71afbb39434a94a1dbee0d85b8ba83.png)
Na questão a) ele que o f de g(x). Então o que faremos? Substituiremos, como fizemos a cima, o x por g(x):
![f[g(x)]=23g(x)^2-1 f[g(x)]=23g(x)^2-1](/latexrender/pictures/bdb8dd951a9a3fb01e5829fb1a3dbea1.png) (f de g(x))
(f de g(x))Só que temos o valor de g(x), então substituiremos g(x) por
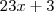
:
![f[g(x)]=23g(x)^2-1 f[g(x)]=23g(x)^2-1](/latexrender/pictures/bdb8dd951a9a3fb01e5829fb1a3dbea1.png)
![f[g(x)]=23*(23x+3)^2-1 f[g(x)]=23*(23x+3)^2-1](/latexrender/pictures/1d5af4d5c6f75a9f6e0c7fefb173fd87.png)
![f[g(x)]=23*(529x^2+138x+9)-1 f[g(x)]=23*(529x^2+138x+9)-1](/latexrender/pictures/342a7aada6ea9a40b611f46ff4c78660.png)
![f[g(x)]=12167x^2+3174x+206 f[g(x)]=12167x^2+3174x+206](/latexrender/pictures/dc31ae7e1a9784f8830f334e6c073d43.png)
E acabou! Agora faça o mesmo procedimento com a letra b)
Qualquer dúvida, escreva aqui!
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por DaniellaFlavia » Dom Mai 30, 2010 16:10
por DaniellaFlavia » Dom Mai 30, 2010 16:10
Em outra questão , tenho

terei de substituir o

pelo valor de

?
-
DaniellaFlavia
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Mai 30, 2010 13:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dificuldades em G.A
 por ogoiD » Seg Mar 22, 2010 17:30
por ogoiD » Seg Mar 22, 2010 17:30
- 4 Respostas
- 3438 Exibições
- Última mensagem por Elcioschin

Qua Abr 14, 2010 13:17
Geometria Analítica
-
- [Probabilidade Condicionada] Dificuldades
 por N0namePT » Sáb Mai 24, 2014 15:44
por N0namePT » Sáb Mai 24, 2014 15:44
- 1 Respostas
- 3210 Exibições
- Última mensagem por Diofanto

Dom Set 14, 2014 23:05
Probabilidade
-
- [Inequaçoes Exponenciais] Grandes Dificuldades
por R0nny » Sáb Mai 11, 2013 20:47
- 0 Respostas
- 705 Exibições
- Última mensagem por R0nny

Sáb Mai 11, 2013 20:47
Equações
-
- Dificuldades em elaborar calculo estatistico
por Giovanna Souza » Qua Dez 11, 2013 11:50
- 0 Respostas
- 3993 Exibições
- Última mensagem por Giovanna Souza

Qua Dez 11, 2013 11:50
Estatística
-
- Tenho dificuldades, preciso de ajudo urgente!!!
por Emanuel » Sáb Abr 03, 2010 10:12
- 3 Respostas
- 2625 Exibições
- Última mensagem por Emanuel

Sáb Abr 03, 2010 13:03
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  , determine:
, determine:![f[g(x)] f[g(x)]](/latexrender/pictures/2b71afbb39434a94a1dbee0d85b8ba83.png)
![g[f(x)] g[f(x)]](/latexrender/pictures/b6b256ffe0a66f87c821c68b1e67258e.png)

 e
e  , determine:
, determine:![f[g(x)] f[g(x)]](/latexrender/pictures/2b71afbb39434a94a1dbee0d85b8ba83.png)
![g[f(x)] g[f(x)]](/latexrender/pictures/b6b256ffe0a66f87c821c68b1e67258e.png)





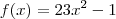 e
e 
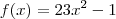 (f de x)
(f de x)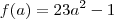 (f de a)
(f de a)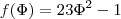 (f de phi)
(f de phi) (f de bolinha)
(f de bolinha)![f[g(x)] f[g(x)]](/latexrender/pictures/2b71afbb39434a94a1dbee0d85b8ba83.png)
![f[g(x)]=23g(x)^2-1 f[g(x)]=23g(x)^2-1](/latexrender/pictures/bdb8dd951a9a3fb01e5829fb1a3dbea1.png) (f de g(x))
(f de g(x))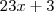 :
:![f[g(x)]=23g(x)^2-1 f[g(x)]=23g(x)^2-1](/latexrender/pictures/bdb8dd951a9a3fb01e5829fb1a3dbea1.png)
![f[g(x)]=23*(23x+3)^2-1 f[g(x)]=23*(23x+3)^2-1](/latexrender/pictures/1d5af4d5c6f75a9f6e0c7fefb173fd87.png)
![f[g(x)]=23*(529x^2+138x+9)-1 f[g(x)]=23*(529x^2+138x+9)-1](/latexrender/pictures/342a7aada6ea9a40b611f46ff4c78660.png)
![f[g(x)]=12167x^2+3174x+206 f[g(x)]=12167x^2+3174x+206](/latexrender/pictures/dc31ae7e1a9784f8830f334e6c073d43.png)



 pelo valor de
pelo valor de  ?
?