 por Dyego » Sex Mar 26, 2010 12:58
por Dyego » Sex Mar 26, 2010 12:58
g(x) = 3 + x + e^x
-
Dyego
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qui Mar 18, 2010 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: cursando
 por 13run0 » Qui Mai 27, 2010 18:45
por 13run0 » Qui Mai 27, 2010 18:45
g(x)=3+x+

. . . eh isso??
então,
y = 3+x+

[subsituindo Y por X . . e X por Y]
x = 3+y+

[isolando o Y]
y = x-3-

[organizando]
y =

+x-3
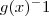
=

+x-3
acredito que seja isso. . .
espero ter ajudado . . .
-
13run0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Mai 27, 2010 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Edificações
- Andamento: formado
 por Molina » Qui Mai 27, 2010 20:45
por Molina » Qui Mai 27, 2010 20:45
13run0 escreveu:g(x)=3+x+

. . . eh isso??
então,
y = 3+x+

[subsituindo Y por X . . e X por Y]
x = 3+y+

[isolando o Y]
y = x-3-

[organizando]
y =

+x-3
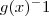
=

+x-3
acredito que seja isso. . .
espero ter ajudado . . .
Boa noite.
Quando você fez a substituição dos X's pelos Y's você esqueceu de substituir o

por

.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por 13run0 » Qui Mai 27, 2010 23:47
por 13run0 » Qui Mai 27, 2010 23:47
Valeu pela observação Molina!
corrigindo então. . .
g(x)=3+x+

então,
y = 3+x+

[subsituindo Y por X . . e X por Y]
x = 3+y+

[isolando o Y]
y = x-3-

[organizando]
y =

+x-3
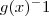
=

+x-3
-
13run0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Mai 27, 2010 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Edificações
- Andamento: formado
 por Molina » Sex Mai 28, 2010 00:00
por Molina » Sex Mai 28, 2010 00:00
De nada, Bruno.
Mas a questão é que a função inversa não pode ficar em função de x e y.
Temos que chegar no final em algo do tipo
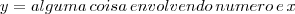
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por 13run0 » Sex Mai 28, 2010 14:17
por 13run0 » Sex Mai 28, 2010 14:17
Então como ficaria essa função inversa?
faz ela aí por favor. . .
-
13run0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Mai 27, 2010 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Edificações
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Qual a função inversa?
por Dyego » Sex Mar 26, 2010 02:26
- 1 Respostas
- 1549 Exibições
- Última mensagem por Elcioschin

Sex Mar 26, 2010 09:41
Funções
-
- Qual é a inversa da função
por andersontricordiano » Sáb Abr 30, 2011 18:44
- 2 Respostas
- 1715 Exibições
- Última mensagem por DanielRJ

Sáb Abr 30, 2011 19:41
Logaritmos
-
- função inversa
por gisa123 » Qui Ago 28, 2008 17:22
- 1 Respostas
- 3397 Exibições
- Última mensagem por Molina

Qui Ago 28, 2008 23:53
Funções
-
- O que é função inversa
por irineu junior » Sex Mar 12, 2010 20:57
- 2 Respostas
- 2642 Exibições
- Última mensagem por irineu junior

Dom Mar 14, 2010 16:28
Funções
-
- Função Inversa
por OtavioBonassi » Qui Jul 14, 2011 23:04
- 6 Respostas
- 7723 Exibições
- Última mensagem por LuizAquino

Sáb Jul 16, 2011 18:14
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 . . . eh isso??
. . . eh isso?? [subsituindo Y por X . . e X por Y]
[subsituindo Y por X . . e X por Y] [isolando o Y]
[isolando o Y] [organizando]
[organizando] +x-3
+x-3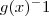 =
=  +x-3
+x-3
. . . eh isso??
[subsituindo Y por X . . e X por Y]
[isolando o Y]
[organizando]
+x-3
=
+x-3
 por
por  .
.

 [subsituindo Y por X . . e X por Y]
[subsituindo Y por X . . e X por Y] [isolando o Y]
[isolando o Y] [organizando]
[organizando] +x-3
+x-3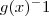 =
=  +x-3
+x-3
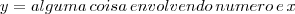



 .
.
 :
: