Bom dia pessoal, gostaria que alguém me ajude a resolver essa equção, estou com um sério problema para lembrar como resolver.
segue a equação:
1,5=e^-0,17/2*8,62X10^-5*298/e^-0,17/2*8,62X10-5*T2
Ln1,5=-0,17/2*8,62X10-5*298+0,17/2*8,62X10-5*T2
depois disso o professor colocou a resposta direta (acho que ele não sabia resolver rs)
T2=339,61 (K)
alguém poderia me ajudar a resolver essa equação? preciso urgente, muito obrigado.




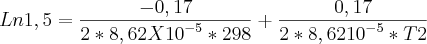
 :
:

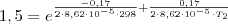
 em ambos os membros a equação, pois é a inversa da exponencial:
em ambos os membros a equação, pois é a inversa da exponencial:
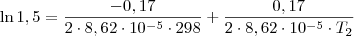

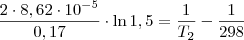

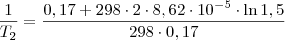
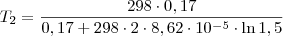
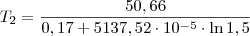

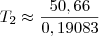
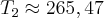
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.