Bom dia pessoal, gostaria que alguém me ajude a resolver essa equção, estou com um sério problema para lembrar como resolver.
segue a equação:
1,5=e^-0,17/2*8,62X10^-5*298/e^-0,17/2*8,62X10-5*T2
Ln1,5=-0,17/2*8,62X10-5*298+0,17/2*8,62X10-5*T2
depois disso o professor colocou a resposta direta (acho que ele não sabia resolver rs)
T2=339,61 (K)
alguém poderia me ajudar a resolver essa equação? preciso urgente, muito obrigado.




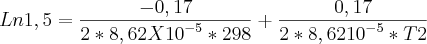
 :
:

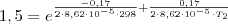
 em ambos os membros a equação, pois é a inversa da exponencial:
em ambos os membros a equação, pois é a inversa da exponencial:
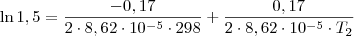

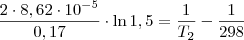

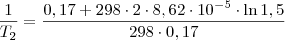
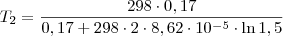
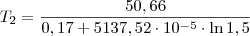

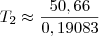
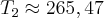

 .
.
 :
: