 por EulaCarrara » Qua Mai 05, 2010 16:14
por EulaCarrara » Qua Mai 05, 2010 16:14
Estou finalizando um capítulo da matéria de derivadas e deparei com o exercício:
- Encontre todos os valores de

nos quais a reta tangente à curva dada satisfaz a propriedade enunciada:
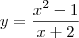
. Horizontal
----
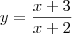
. Perpendicular à reta

.
São vários, porém parecidos.. Peguei os 02 mais "diferentes".
Agradeço a quem puder ajudar.

-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por EulaCarrara » Qua Mai 05, 2010 17:10
por EulaCarrara » Qua Mai 05, 2010 17:10
-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por EulaCarrara » Qua Mai 05, 2010 19:22
por EulaCarrara » Qua Mai 05, 2010 19:22
Alguém please :~
-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por Molina » Qua Mai 05, 2010 20:55
por Molina » Qua Mai 05, 2010 20:55
Boa noite.
EulaCarrara escreveu: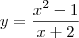
. Horizontal
A reta tangente horizontal significa que a derivada é
zero.
Então derive y e iguale a 0. Os valores de x que satisfazem essa equação é a resposta do seu problema!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por EulaCarrara » Qua Mai 05, 2010 21:05
por EulaCarrara » Qua Mai 05, 2010 21:05
Olá molina! Obrigada! Eu não tinha pensado nisso...
Mas e quanto à perpedicularidade de:
EulaCarrara escreveu: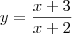
. Perpendicular à reta

-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por EulaCarrara » Qua Mai 05, 2010 22:23
por EulaCarrara » Qua Mai 05, 2010 22:23
-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por Molina » Qui Mai 06, 2010 00:15
por Molina » Qui Mai 06, 2010 00:15
EulaCarrara escreveu: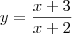
. Perpendicular à reta

A reta

tem reta tangente igual a 1.
(alguma dúvida?)Como ele quer perpendicular a

, então a reta tangente tem que ser -1.
Isso é mais fácil de ver se você perceber que as retas

e
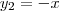
são perpendiculares.
Finalizando, iguale y a -1.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10896 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13201 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14806 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5116 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 nos quais a reta tangente à curva dada satisfaz a propriedade enunciada:
nos quais a reta tangente à curva dada satisfaz a propriedade enunciada: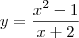 . Horizontal
. Horizontal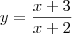 . Perpendicular à reta
. Perpendicular à reta 

 nos quais a reta tangente à curva dada satisfaz a propriedade enunciada:
nos quais a reta tangente à curva dada satisfaz a propriedade enunciada: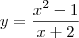 . Horizontal
. Horizontal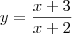 . Perpendicular à reta
. Perpendicular à reta 



. Horizontal


. Perpendicular à reta


. Perpendicular à reta
 tem reta tangente igual a 1. (alguma dúvida?)
tem reta tangente igual a 1. (alguma dúvida?) , então a reta tangente tem que ser -1.
, então a reta tangente tem que ser -1. e
e 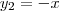 são perpendiculares.
são perpendiculares.


 .
.
 :
: