 por Soprano » Qui Mar 03, 2016 09:17
por Soprano » Qui Mar 03, 2016 09:17
Olá a todos,
O objectivo do exercico é encontrar o conjunto de solução da equações de segundo grau (função quadrática). Posso aplicar o produto da soma pela diferença desta forma?
2x²+2x-12=0
2(x²+x-6)
2(x-2)(x+3)
x-2=0 v x+3=0
x=2 v x=-3
Não estou a conseguir resolver o exercicio sem aplicar assim o produto da soma pela diferença.
Obrigado
-
Soprano
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Fev 14, 2016 10:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Electrónica
- Andamento: cursando
 por DanielFerreira » Sáb Mar 05, 2016 05:02
por DanielFerreira » Sáb Mar 05, 2016 05:02
Olá!
Tua resposta está correcta!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Soprano » Seg Mar 07, 2016 12:57
por Soprano » Seg Mar 07, 2016 12:57
Obrigado pela resposta,
Sempre pensei que o produto da soma pela diferença apenas podesse ser exposto desta forma (x+a)(x-b). Mas depois fiz os calculos com ambos os modelos, (x+a)(x-b) e (x-a)(x-b), e descobri que era o mesmo!
Mas isto faz sentido?
(x+5)(x-9) = x²-4x-45
(x-5)(x+9) = x²+4x-45
Ou não é possível?
-
Soprano
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Fev 14, 2016 10:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Electrónica
- Andamento: cursando
 por DanielFerreira » Ter Mar 08, 2016 21:47
por DanielFerreira » Ter Mar 08, 2016 21:47
Soprano, boa noite!
Inicialmente, tomemos como exemplo os números

e

. O produto da soma pela diferença entre eles é dado por:

Supomos agora que os números em questão não sejam conhecidos; sejam

e

tais números, então o produto da soma pela diferença é dado por
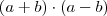
.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Diferença entre os produto escalar.
por 380625 » Seg Ago 15, 2011 19:43
- 1 Respostas
- 1744 Exibições
- Última mensagem por LuizAquino

Seg Ago 15, 2011 21:32
Geometria Analítica
-
- transformar soma em produto
por Rhadys » Ter Jun 21, 2011 15:08
- 3 Respostas
- 3171 Exibições
- Última mensagem por Claudin

Qua Jun 22, 2011 01:34
Trigonometria
-
- Soma e produto das raizes das equações.
por Thays » Ter Jan 22, 2013 12:41
- 3 Respostas
- 4159 Exibições
- Última mensagem por Thays

Qua Jan 23, 2013 10:11
Equações
-
- Problema equação de 2 grau - soma e produto
por melned » Ter Mar 10, 2009 16:17
- 1 Respostas
- 2644 Exibições
- Última mensagem por Marcampucio

Ter Mar 10, 2009 19:50
Sistemas de Equações
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5562 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e
e  . O produto da soma pela diferença entre eles é dado por:
. O produto da soma pela diferença entre eles é dado por: 
 e
e  tais números, então o produto da soma pela diferença é dado por
tais números, então o produto da soma pela diferença é dado por 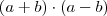 .
.