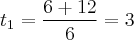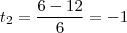Preciso de ajuda no seguinte exercício:
"Uma pedra é lançada verticalmente para cima. Sua altura h (metros) em relação ao solo, é dada por
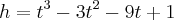, onde t indica o número de segundos decorridos após o lançamento. Em que instante a pedra atingirá sua altura máxima?"Bom, como queremos encontrar o instante no qual a pedra atinge altura máxima, queremos, então, encontrar o ponto de máximo global. Daí, derivei a função f(t) = h. Fazendo um estudo do sinal, vem que t = -1 é o instante procurado. Contudo, isto não faz sentido. O instante é negativo. Daí, observando o gráfico da f, [url]http://www.wolframalpha.com/input/?i=f%28t%29+%3D+%28%28t%29^%283%29%29+-+%28%283%29%28%28t%29^%282%29%29%29+-+9t+%2B1[/url], vem que a função explode. O instante t = -1 realmente é ponto de máximo, mas, local. Agora, eu não entendi. O que estou fazendo de errado?
Por favor, preciso de ajuda!!
Muito Obrigada!
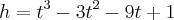
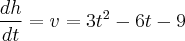
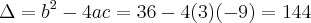
![t =\frac{ -b \pm \sqrt[]{\Delta}}{2a} = \frac{-(-6) \pm \sqrt[]{144}}{2(3)} = \frac{6\pm 12}{6}](/latexrender/pictures/be8e1da667a8cff161af6e772c462d92.png "t =\frac{ -b \pm \sqrt[]{\Delta}}{2a} = \frac{-(-6) \pm \sqrt[]{144}}{2(3)} = \frac{6\pm 12}{6}")
por 
.
, 
e para 
, 
.
e 
, monte a função e substitua 
por 
.
