Preciso de ajuda num exercício.
"Prove que o grupo de Klein e
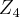 não são isomorfos."
não são isomorfos."Eu sei que o grupo de Klein apresenta quatro elementos, sendo um deles o elemento neutro, e tais que a cada dois operados entre si, resulta no terceiro. Daí, como o exercício não especifica os elementos, tomei um genérico:
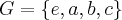 . Já o
. Já o 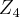 é o grupo das classes de restos, ou seja,
é o grupo das classes de restos, ou seja, 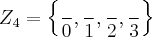 . O problema é que, para mim, devemos mostrar que uma
. O problema é que, para mim, devemos mostrar que uma 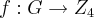 é homomorfismo bijetor. Mas, como fazer isso se o exercício não informa qual é a lei da f e muito menos as operações envolvidas ?! Pode ser burrice minha não saber disso, mas nem mesmo o livro mostra como resolver este tipo de exercício. Todos os exemplos são com f definidas, operações definidas. O livro sugere: "Tomar um possível homomofismo f e mostrar que não é bijetora".
é homomorfismo bijetor. Mas, como fazer isso se o exercício não informa qual é a lei da f e muito menos as operações envolvidas ?! Pode ser burrice minha não saber disso, mas nem mesmo o livro mostra como resolver este tipo de exercício. Todos os exemplos são com f definidas, operações definidas. O livro sugere: "Tomar um possível homomofismo f e mostrar que não é bijetora".Por favor, eu imploro por ajuda! O professor vai ficar bravo se eu perguntar, vai rir de mim. A internet não está ajudando. O livro faz apenas uma sugestão que pra mim não está fazendo sentido. Por favor, eu não sei mais o que fazer! Por favor, ajudem!!!!!!!!!!


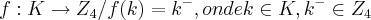 logo teremos
logo teremos 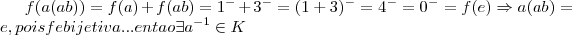 tal q.
tal q. 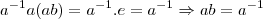 q. e uma contradiçao pois os elementos de K, so admite inverso(inverso multiplicativo ou simetrico aditivo)dele proprio...logo por f,K nao e isomorfo com
q. e uma contradiçao pois os elementos de K, so admite inverso(inverso multiplicativo ou simetrico aditivo)dele proprio...logo por f,K nao e isomorfo com 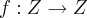 ,f bijetiva e isomorfa em Z, nao possue a propriedade q. expus,a saber...f(n.m)=f(n)+f(m),e sim os homorfismos f(n.m)=f(n).f(m),f(n+m)=f(n)+f(m),entao...
,f bijetiva e isomorfa em Z, nao possue a propriedade q. expus,a saber...f(n.m)=f(n)+f(m),e sim os homorfismos f(n.m)=f(n).f(m),f(n+m)=f(n)+f(m),entao... ,com f e bijetiva teremos...
,com f e bijetiva teremos...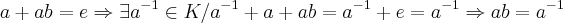 ,o q. e uma contradiçao em K...entao por f, K nao e isomorfo a
,o q. e uma contradiçao em K...entao por f, K nao e isomorfo a  (prove como exercicios) e
(prove como exercicios) e 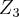 (esse muito dificil),estude mais e vc compreendera a resoluçao...
(esse muito dificil),estude mais e vc compreendera a resoluçao...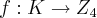 ...tomei f(n)=n,q. e bijetiva e um homomorfismo em Z,para mostrar q. K nao eh isomorfismo em
...tomei f(n)=n,q. e bijetiva e um homomorfismo em Z,para mostrar q. K nao eh isomorfismo em 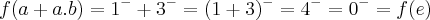 ,onde
,onde 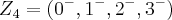 ,
,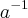 ,tal q.
,tal q. 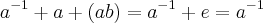 ,
,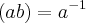 o q. nos leva a uma contradiçao,pois os elementos de K,somente admitem inverso(ou simetrico) deles proprios...entao K nao e isomorfo a
o q. nos leva a uma contradiçao,pois os elementos de K,somente admitem inverso(ou simetrico) deles proprios...entao K nao e isomorfo a 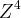 ...provamos usando a funçao bijetiva f
...provamos usando a funçao bijetiva f
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.