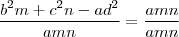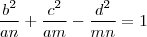por matheus_frs1 » Dom Nov 02, 2014 19:54
por matheus_frs1 » Dom Nov 02, 2014 19:54
Galera, o teorema de Stewart é expresso pela famosa fórmula
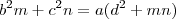
, sendo

a ceviana. Porém nas aulas do nerckie eu vi a seguinte relação equivalente:

O problema é que eu não consegui passar da primeira pra segunda fórmula, queria saber essa conversão algebricamente, alguém me ajuda?
Obrigado
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Russman » Dom Nov 02, 2014 21:40
por Russman » Dom Nov 02, 2014 21:40
É simples.
Da expressão
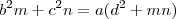
efetua a multiplicação em

, passe o termo
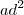
para o 1° membro e divida toda a expressão por

.


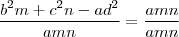
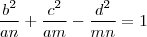
Voilà.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por matheus_frs1 » Dom Nov 02, 2014 23:52
por matheus_frs1 » Dom Nov 02, 2014 23:52
kkkkkkkkkkkkk credo, fiquei até envergonhado de tão fácil que é agora q vi a resolução. Acho q não me atentei pro denominador comum no primeiro membro, posso quebrar aquela soma no numerador em várias somas de frações com o mesmo denominador e cortar oq tem q ser cortado. Vlw mais uma vez, Russman, salvando mais vidas que o Goku.
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Russman » Seg Nov 03, 2014 00:10
por Russman » Seg Nov 03, 2014 00:10
Hahahah. É, apenas uma questao de "cair a ficha".
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada: Livro Stewart
por leandro_aur » Sáb Ago 13, 2011 16:14
- 3 Respostas
- 2434 Exibições
- Última mensagem por LuizAquino

Sáb Ago 13, 2011 21:23
Cálculo: Limites, Derivadas e Integrais
-
- Problemas Quentes do Livro do James Stewart
por ARCS » Dom Fev 12, 2012 00:11
- 1 Respostas
- 3726 Exibições
- Última mensagem por fraol

Dom Fev 12, 2012 10:44
Cálculo: Limites, Derivadas e Integrais
-
- Possível erro de digitação no Stewart 5ª edição!
por ravi » Sex Jan 18, 2013 03:11
- 2 Respostas
- 3108 Exibições
- Última mensagem por ravi

Sex Jan 18, 2013 13:15
Cálculo: Limites, Derivadas e Integrais
-
- fórmula
por Ismafa » Ter Fev 17, 2009 01:29
- 2 Respostas
- 3228 Exibições
- Última mensagem por Ismafa

Qua Fev 25, 2009 09:57
Sistemas de Equações
-
- Fórmula de PMT
por Leonardonc » Seg Ago 27, 2012 09:27
- 0 Respostas
- 2280 Exibições
- Última mensagem por Leonardonc

Seg Ago 27, 2012 09:27
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
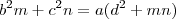 , sendo
, sendo  a ceviana. Porém nas aulas do nerckie eu vi a seguinte relação equivalente:
a ceviana. Porém nas aulas do nerckie eu vi a seguinte relação equivalente: 

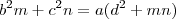 , sendo
, sendo  a ceviana. Porém nas aulas do nerckie eu vi a seguinte relação equivalente:
a ceviana. Porém nas aulas do nerckie eu vi a seguinte relação equivalente: 

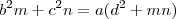
 , passe o termo
, passe o termo 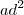 para o 1° membro e divida toda a expressão por
para o 1° membro e divida toda a expressão por  .
.