 por neoreload » Sáb Nov 01, 2014 08:25
por neoreload » Sáb Nov 01, 2014 08:25
Pessoal como resolver essa:
Encontre a derivada da função
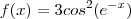
Eu até achava fácil, porém ao tentar fazer com a formula
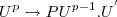
o resultado que eu chego é bem diferente da resposta que tem na apostila(resposta em anexo). Se possível deixar bem detalhado o passo a passo para que eu possa entender onde que estou errando, obrigado ^^
Resposta:

-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por young_jedi » Sáb Nov 01, 2014 12:06
por young_jedi » Sáb Nov 01, 2014 12:06
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por neoreload » Sáb Nov 01, 2014 17:48
por neoreload » Sáb Nov 01, 2014 17:48
Entendo, mas pq nesse caso em especifico eu preciso usar duas vezes ?
-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por young_jedi » Dom Nov 02, 2014 09:28
por young_jedi » Dom Nov 02, 2014 09:28
é porque você tem a função

dentro da função

e a função

dentro da função
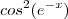
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por neoreload » Dom Nov 02, 2014 10:14
por neoreload » Dom Nov 02, 2014 10:14
young_jedi escreveu:é porque você tem a função

dentro da função

e a função

dentro da função
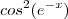
Muito obrigado amigo, agora entendi ^^. Só uma coisa, então o gabarito está errado não é? pois lá tem o 6 como -6 no final. Obrigado mais uma vez ^^
-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por young_jedi » Dom Nov 02, 2014 10:29
por young_jedi » Dom Nov 02, 2014 10:29
É verdade, mas o sinal de menos acho que é um erro de gabarito mesmo.
Valeu !
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] - Derivada de função partida (e indeterminação)
por AlexanderCanust » Qui Mai 28, 2015 12:10
- 0 Respostas
- 1369 Exibições
- Última mensagem por AlexanderCanust

Qui Mai 28, 2015 12:10
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Derivadas parciais
por -civil- » Qui Set 29, 2011 15:28
- 1 Respostas
- 2080 Exibições
- Última mensagem por LuizAquino

Sex Set 30, 2011 17:57
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Questão simples de derivada.
por Gustavo195 » Ter Mai 14, 2013 17:52
- 0 Respostas
- 1591 Exibições
- Última mensagem por Gustavo195

Ter Mai 14, 2013 17:52
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Derivadas parciais e ponto crítico
por Mell » Dom Jul 07, 2013 10:24
- 1 Respostas
- 1911 Exibições
- Última mensagem por hygorvv

Seg Jul 08, 2013 07:11
Cálculo: Limites, Derivadas e Integrais
-
- [derivadas ]essa derivada já ta esquentando minha cabeça.
por vinicastro » Sáb Dez 15, 2012 22:42
- 5 Respostas
- 2981 Exibições
- Última mensagem por vinicastro

Dom Dez 16, 2012 15:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
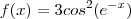
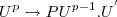 o resultado que eu chego é bem diferente da resposta que tem na apostila(resposta em anexo). Se possível deixar bem detalhado o passo a passo para que eu possa entender onde que estou errando, obrigado ^^
o resultado que eu chego é bem diferente da resposta que tem na apostila(resposta em anexo). Se possível deixar bem detalhado o passo a passo para que eu possa entender onde que estou errando, obrigado ^^










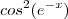

 .
.
 :
: