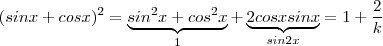por Antonio Unwisser » Dom Set 28, 2014 16:39
por Antonio Unwisser » Dom Set 28, 2014 16:39
Boa tarde, pessoal.
Simplesmente não consigo resolver exercícios que propõem que se ache o resultado de uma determinada operação a partir do resultado de outra.
Por exemplo:
Sabendo que
cossec x/sec x + sec x/cossec x = 5, o valor de
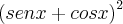
é:
Ou então:
Se tg x + cotg x = 3, calcule sen 2x.
Estou com todas as identidades (cossec x = 1/sen x; etc.) em mente, bem como as fórmulas derivadas da Relação Fundamental, e também mantendo em mente que
sen 2x = 2senx.cosx, e cos 2x =

-
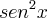
, e as outras que se derivam a partir daí, bem como as da tangente.
Mas obviamente há alguma relação que não consigo enxergar. Qualquer ajuda será muito bem-vinda.
Obrigado pela atenção.
-
Antonio Unwisser
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 30, 2014 20:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Filosofia
- Andamento: cursando
 por e8group » Dom Out 05, 2014 21:42
por e8group » Dom Out 05, 2014 21:42
Não há uma regra geral p/ resolver estes tipos de equações , e destes casos expostos o objetivo não é resolver a eq. primeiro p/ x e depois computar sin 2x , etc ...A ideia é reescrever estas equações em termos de sin 2x ou de sin x + cos x .. Veremos como isto é possível ...
Vou propor uma equação , escolha algum número real k (a princípio sem restrições ) , fixado a escolha seja a eq.
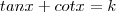
. Se você fizer k = 5 e depois igual 3 você terá exatamente as duas equações que expôs (certifique-se que o primeiro membro da 1ª eq. é o mesmo que o escrever tan x + cot x .) .
Agora note que
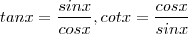
.
Daí ,
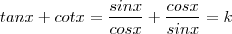
. Ou ainda ,

.Mas
sabemos da relação trigonométrica que

e também que
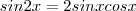
. Assim ,

o que implica
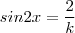
. Segue daí que podemos escolher qualquer k maior ou igual a 2 em módulo (pois seno é limitado por 1) .
Em particular , com k = 5 , tem a resposta desejada . Agora p/ computar

note que
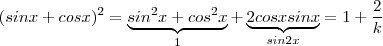
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Antonio Unwisser » Seg Out 06, 2014 19:43
por Antonio Unwisser » Seg Out 06, 2014 19:43
Muitíssimo obrigado, santhiago.


Antônio.
-
Antonio Unwisser
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 30, 2014 20:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Filosofia
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplifique a expressão com radicais duplos
por Balanar » Seg Ago 09, 2010 04:01
- 2 Respostas
- 59280 Exibições
- Última mensagem por Soprano

Sex Mar 04, 2016 09:49
Desafios Difíceis
-
- Simplifique a expressão com radicais duplos abaixo:
por Bryan Sales » Dom Jul 20, 2014 19:11
- 1 Respostas
- 3541 Exibições
- Última mensagem por Soprano

Sex Mar 04, 2016 09:51
Aritmética
-
- Dúvida,relação binária
por ibatexano » Sex Set 18, 2009 16:15
- 2 Respostas
- 5991 Exibições
- Última mensagem por ibatexano

Sex Set 18, 2009 23:14
Álgebra
-
- Duvida com relação a integral
por MarceloRocks » Seg Dez 03, 2012 11:31
- 1 Respostas
- 3106 Exibições
- Última mensagem por young_jedi

Seg Dez 03, 2012 15:54
Funções
-
- [Simplificação] Dúvida em relação ao resultado
por stilobreak » Sáb Mar 23, 2013 02:43
- 1 Respostas
- 3116 Exibições
- Última mensagem por DanielFerreira

Sex Mar 29, 2013 02:20
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
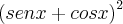 é:
é: -
- 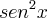 , e as outras que se derivam a partir daí, bem como as da tangente.
, e as outras que se derivam a partir daí, bem como as da tangente. 

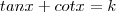 . Se você fizer k = 5 e depois igual 3 você terá exatamente as duas equações que expôs (certifique-se que o primeiro membro da 1ª eq. é o mesmo que o escrever tan x + cot x .) .
. Se você fizer k = 5 e depois igual 3 você terá exatamente as duas equações que expôs (certifique-se que o primeiro membro da 1ª eq. é o mesmo que o escrever tan x + cot x .) . 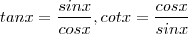 .
. 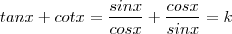 . Ou ainda ,
. Ou ainda ,  .Mas
.Mas  e também que
e também que 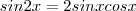 . Assim ,
. Assim ,  o que implica
o que implica 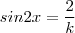 . Segue daí que podemos escolher qualquer k maior ou igual a 2 em módulo (pois seno é limitado por 1) .
. Segue daí que podemos escolher qualquer k maior ou igual a 2 em módulo (pois seno é limitado por 1) . note que
note que