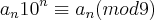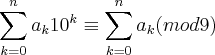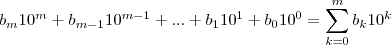Ok, agora não dá mais pra escapar da aritmetica modular...
Partiu: N é um número da forma:
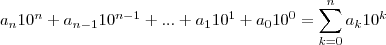
Sendo
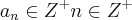
Ok, e temos que, pela congruência,
 (1)
(1)A forma do número N (a qual todos os números inteiros assumem) vai nos ajudar a ver que, sendo N congruente à 1 módulo 9 (-1 elevado a par, elevado a par, elevado a par... etc... é igual a 1) a soma dos seus algarismos também é.
Vejamos bem: pegando uma potência de 10 e seu coeficiente, vemos que dividido por 9, o resto é 1xcoeficiente. Correto? (pois o resto da divisão de uma potencia de 10 por 9 é sempre 1 e o resto da divisão de um coeficiente qualquer por 9 supomos que seja ele mesmo, para efeito de desembaraço).
Temos então que a soma dos algarismos de N (no caso, os coeficiente acima citados) é também congruente a 1 módulo 9.
Pois:
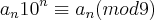
Então:
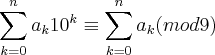
E, pela definição dada em (1), temos:

Vemos que a soma dos algarismos resulta em M, que comprovadamente (penso eu) é congruente a 1 módulo 9.
O numero M, não diferentemente de N, tem a forma:
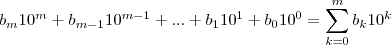
Rapaziada, fazendo um raciocínio análogo, vamos ficar pra sempre nessa recorrência, até que sobre apenas um coeficiente, que pela congruência, dá 1.
Ufa! Espero que seja isso aí. heheheh
Qualquer coisa, comentem.
Abraços













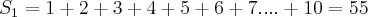

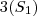 -->
--> 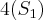 -->
--> 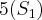 .....
..... 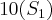



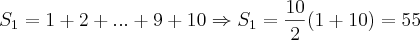
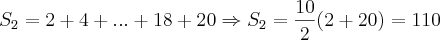
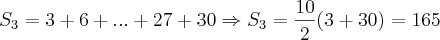
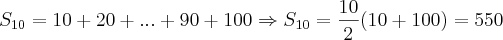
 como:
como: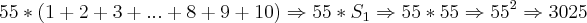









 , isso implica dizer que 12 = 21?
, isso implica dizer que 12 = 21?  e pela propriedade da função,
e pela propriedade da função,  e por aí vai....
e por aí vai....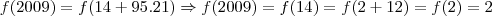

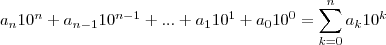
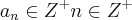
 (1)
(1)