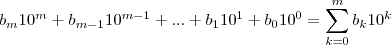Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Molina » Qui Jun 11, 2009 22:03
por Molina » Qui Jun 11, 2009 22:03
Semana passada, ocorreu em vários estados brasileiros a Olimpíada Brasileira de Matemática. Pra quem nunca teve contato com esse tipo de prova, no primeiro momento vai parecer um pouco difícil. Mas a idéias da organização é fazer questões que podem ser resolvidas realmente por um modo mais trabalhoso mas também podem ser resolvida por através de um pensamento diferenciado.
Vou colocar aqui duas questões do nível 3.
Espero que gostem, 

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Sex Jun 12, 2009 08:41
por Cleyson007 » Sex Jun 12, 2009 08:41
Bom dia Molina!
Essas questões da OBM são muito bem elaboradas

Vou dar o meu palpite (talvez esteja errado) quanto a questão 01.
Acho que a alternativa
a é falsa, pois o enunciado diz que Agilulfo não foi colocado de castigo ontem.
Acho que a alternativa
b não é certamente verdadeira, uma vez que não sabemos se a mãe do Agilulfo encontrava-se em casa na hora de sua chegada.
Acho que a alternativa c é falsa, pois o enunciado diz que Agilulfo não foi colocado de castigo (é sinal que voltou para casa sem advertência), portanto não sabemos se sua mãe estava em casa. (Esse pensamento acaba explicando a alternativa
d que também parece ser falsa).
Acho que a alternativa correta é a e.
Bom... essa é minha opinião.. vamos ver o que os usuários do fórum acham
 --> Qual é a sua opinião Molina?
--> Qual é a sua opinião Molina? Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Neperiano » Sex Jun 12, 2009 20:03
por Neperiano » Sex Jun 12, 2009 20:03
Ola
Eu fiz essa prova no meu Colégio, e considerei ela parelha com um vestibular, mas um pouco mais complexo.
Quantos as questões Cleyson é sim E a questão que voçe resolveu.
Abraços
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sex Jun 12, 2009 20:13
por Molina » Sex Jun 12, 2009 20:13
Boa noite, Cleyson e Maligno.
Eu também colocaria alternativa
e, justamente do modo que provavelmente vocês dois fizeram: através de eliminação.
Alguém se habilita a fazer a segunda questão? Entenderam o enunciado ou precisam de alguma ajuda?
Maligno, você conseguiu fazer esta na prova?
Abraços e to gostando de ver dos forenses..

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Sex Jun 12, 2009 20:34
por Cleyson007 » Sex Jun 12, 2009 20:34
Boa noite Diego Molina.
Essa questão nº 02 é mais difícil

Vou explicar o meu raciocínio:
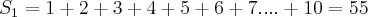

A sequência segue...
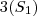
-->
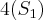
-->
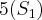
.....
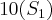

Estou encontrando
Alternativa B, está correto?
Até mais.
Um abraço.
Editado pela última vez por
Cleyson007 em Sex Jun 12, 2009 20:37, em um total de 2 vezes.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Neperiano » Sex Jun 12, 2009 20:35
por Neperiano » Sex Jun 12, 2009 20:35
Ola
Consegui sim
Vo espera se ninguem conseguir responder
Eu respondo e explico
Abraços
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sex Jun 12, 2009 21:09
por Molina » Sex Jun 12, 2009 21:09
Boa noite, Cleyson e Maligno.
Obrigado pela rápida resposta.
Vou colocar aqui um método que eu faria (Usando Soma de PA):
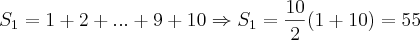
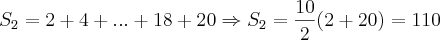
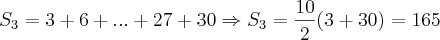
.
.
.
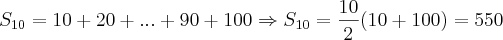
Como bem observado pelo Cleyson, podemos escrever

como:
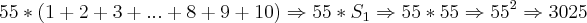
Amanha disponibilizo mais duas questões que considero interessante.
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Sex Jun 12, 2009 22:44
por Neperiano » Sex Jun 12, 2009 22:44
Ola
Poise é esse o jeito que eu fiz, e iria explicar mas voçe ja colocou entaum tah tudo ok
A resposta é para estar certa
Abraços
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Dom Jun 14, 2009 14:40
por Molina » Dom Jun 14, 2009 14:40
Como foi dito anteriormente, segue em anexo mais 2 questões do Nível 3.


- Anexos
-

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por figueroa » Seg Set 07, 2009 22:06
por figueroa » Seg Set 07, 2009 22:06
na primeira questão dessas 2 do nivel 3 que vc postiou eu enconrei 1 como resposta, mas ta no gabarito do site da OBM que a resposta é 2.
olha como eu fiz :
f(7) = f(21+7) = f(21+21+7) = ...= f(7+(n-1)21) , como f(95*21+7) = f(2009) então f(2009) = f(7+(n-1)21)
f(1) = f(1+12) = f(1+12+12) =...= f(1+(n-1)12) = 1
agora repare: se 7+(x-1)21 = 1+(y-1)12 então f(7+(x-1)21) = f(1+(y-1)12)
7+(x-1)21 = 1+(y-1)12 tem solução, por exemplo, x=3 e y=5 daí f(7+(x-1)21) = f(1+(y-1)12) = f(49) = 1
como f(2009) = f(7+(n-1)21) e f(7+(x-1)21) = 1 então f(2009) = 1
não vejo erro em meu raciocínio, acho que estou certo tb.
Edit: encontrei o erro infantil que cometi 95*21+7= 2002 e não 2009

-
figueroa
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Set 08, 2008 14:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: cursando engenharia de produção e física
- Andamento: cursando
 por Molina » Qua Set 09, 2009 00:36
por Molina » Qua Set 09, 2009 00:36
Dificilmente eles erram no gabarito, Figueroa.
Mas acontece, né?
Porém, não foi desta vez...

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por BlackFoxes » Sáb Dez 26, 2009 06:38
por BlackFoxes » Sáb Dez 26, 2009 06:38
Olá, boa madrugada para todos. Vamos dar uma olhada nessas funções..
É dado que

, isso implica dizer que 12 = 21?
NÃO!!!
Vamos aproveitar essa propriedade dada no enunciado para mostrar que podemos ir "cortando" os múltiplos de 12 e 21 até chegar a um dos valores da variável x para os quais temos a imagem...
Por exemplo:

e pela propriedade da função,

e por aí vai....
Arrancando os múltiplos de 12 e 21 do valor 2009 até sobrar um resultado notável resolveremos a questão.
Partiu então:
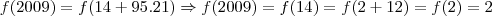
Resposta letra C.
Qualquer incongruência lógica na minha resolução, por favor apontem.
Abraços
Obs.: Eu fiz as contas com calculadora, e por isso peço desculpas. Tenho certeza que com aritmética modular sai mais fácil, mas a preguiça falou mais alto...
-
BlackFoxes
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Dez 26, 2009 04:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por BlackFoxes » Sáb Dez 26, 2009 07:44
por BlackFoxes » Sáb Dez 26, 2009 07:44
Ok, agora não dá mais pra escapar da aritmetica modular...
Partiu: N é um número da forma:
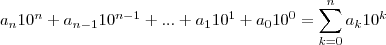
Sendo
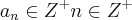
Ok, e temos que, pela congruência,
 (1)
(1)A forma do número N (a qual todos os números inteiros assumem) vai nos ajudar a ver que, sendo N congruente à 1 módulo 9 (-1 elevado a par, elevado a par, elevado a par... etc... é igual a 1) a soma dos seus algarismos também é.
Vejamos bem: pegando uma potência de 10 e seu coeficiente, vemos que dividido por 9, o resto é 1xcoeficiente. Correto? (pois o resto da divisão de uma potencia de 10 por 9 é sempre 1 e o resto da divisão de um coeficiente qualquer por 9 supomos que seja ele mesmo, para efeito de desembaraço).
Temos então que a soma dos algarismos de N (no caso, os coeficiente acima citados) é também congruente a 1 módulo 9.
Pois:
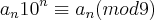
Então:
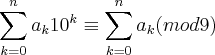
E, pela definição dada em (1), temos:

Vemos que a soma dos algarismos resulta em M, que comprovadamente (penso eu) é congruente a 1 módulo 9.
O numero M, não diferentemente de N, tem a forma:
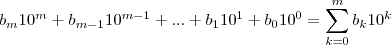
Rapaziada, fazendo um raciocínio análogo, vamos ficar pra sempre nessa recorrência, até que sobre apenas um coeficiente, que pela congruência, dá 1.
Ufa! Espero que seja isso aí. heheheh
Qualquer coisa, comentem.
Abraços
-
BlackFoxes
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Dez 26, 2009 04:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- OBM - Nível 1
 por Molina » Qui Jun 11, 2009 21:38
por Molina » Qui Jun 11, 2009 21:38
- 3 Respostas
- 2874 Exibições
- Última mensagem por Molina

Dom Jun 14, 2009 14:38
Desafios Fáceis
-
- OBM - Nível 2
 por Molina » Qui Jun 11, 2009 21:51
por Molina » Qui Jun 11, 2009 21:51
- 7 Respostas
- 4182 Exibições
- Última mensagem por Cleyson007

Seg Jun 15, 2009 10:20
Desafios Médios
-
- Nível fácil - FCC e UPE
por ingridgusmao » Dom Jun 12, 2011 02:41
- 1 Respostas
- 7533 Exibições
- Última mensagem por nietzsche

Sex Jun 24, 2011 22:54
Conjuntos
-
- Nível de uma represa
por Andreza » Seg Nov 14, 2011 14:54
- 1 Respostas
- 1451 Exibições
- Última mensagem por MarceloFantini

Seg Nov 14, 2011 19:21
Sequências
-
- curvas de nível
por Silva339 » Qua Mai 22, 2013 18:16
- 0 Respostas
- 1472 Exibições
- Última mensagem por Silva339

Qua Mai 22, 2013 18:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.













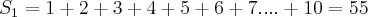

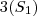 -->
--> 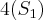 -->
--> 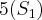 .....
..... 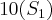



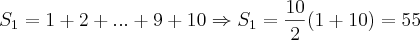
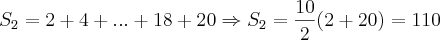
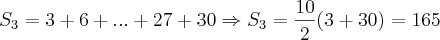
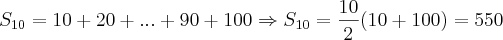
 como:
como: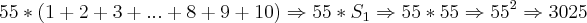









 , isso implica dizer que 12 = 21?
, isso implica dizer que 12 = 21?  e pela propriedade da função,
e pela propriedade da função,  e por aí vai....
e por aí vai....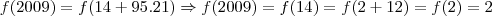

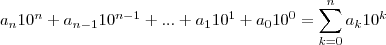
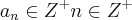
 (1)
(1)