 por CJunior » Qui Jun 19, 2014 15:42
por CJunior » Qui Jun 19, 2014 15:42
Olá pessoal, eu estou com muita dúvida na questão abaixo, não sei nem como começar a responder!!!
Sejam

e

,
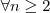
. Se

para

, prove que
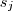
tem, no mínimo,
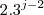
divisores positivos,
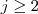
.
Eu gostaria também que vocês me indicassem algum material bom e gratuito, especialmente em pdf e de caráter introdutório, pelo qual eu aprenderei a resolver problemas que envolvam sequências, como o problema acima, recorrências e produtos e somas telescópicas a nível olímpico(nível 2). Desde já, muito obrigado!!!
-
CJunior
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Dom Jan 26, 2014 13:18
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por e8group » Sex Jun 20, 2014 01:24
por e8group » Sex Jun 20, 2014 01:24
Segue minha dicas .
Proposta 1 : Indução Matemática . Está familiarizado com indução ?
Proposta 2 . Para
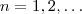
,segue-se que
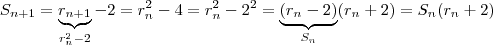
(Fórmula recursiva ) equivalentemente
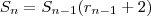
para
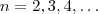
.
Podemos utilizar a fórmula recursiva para escrever

em função de

(a fórmula é válida sempre que o índice
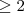
) .Assim , por exemplo

. Em geral , tem-se
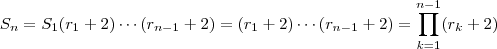
.
Deixe

, então

.
A ideia agora é encontrar todos números

(distintos) que é escrito como produto de

termos distintos da lista

para
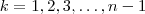
.A pergunta é , escolhendo-se

números acima dentro dos

, quanto números

teremos ?? A respota p/ está pergunta será a quantidade mínima [/tex] .
Para cada
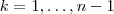
. Temos que a quantidade de k-uplas da forma
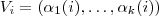
de modo que
![[\alpha_1(i) \cdots \alpha_k(i) ] \neq [\alpha_1(j) \cdots \alpha_k(j) ] \forall i\neq j [\alpha_1(i) \cdots \alpha_k(i) ] \neq [\alpha_1(j) \cdots \alpha_k(j) ] \forall i\neq j](/latexrender/pictures/423edf12a4f723dc7d64384e7e303491.png)
, com

sendo algum dos

é

que é a mesma quantidade de produtos distintos da forma
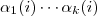
.
Logo , o n° mínimo requerido é

e

.
Desde que ,
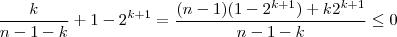
Segue-se que
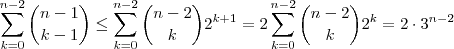
.
Aí fica minhas sugestões ; acho que a
proposta 1 é mais adequada .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sex Jun 20, 2014 12:12
por e8group » Sex Jun 20, 2014 12:12
Na verdade , errei na digitação .
O certo seria
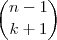
e não

...
Aproveitando os cálculos basta trocar k por k+2 e manipular combinação em função da de n-2 a k ; mesmo assim a desigualdade é válida . Além disso , há mais divisores ; pois
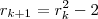
sempre que
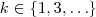
, então
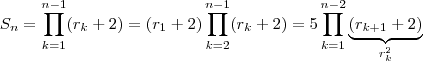
sempre que
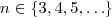
. Por este lado , nota-se que algum dos divisores de

são escritos como

com
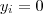
ou

.
Todos estes números certamente dividem

. Se analisar todas as possibilidades juntamente com aquelas que já fizemos somando-se obterá um n° que é menor o igual
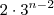
(se não errei contas ) ; logo este número sempre cumpre com o mínimo requerido .Mas vale ressaltar a importância de usar a indução matemática , essa sim é mais é mais precisa e formal . Pode-se que fizemos algumas afirmações que não cumprem com os termos depois dos "..." , pq não ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sequencia] Calcular limite de sequencia por definição
 por amigao » Ter Abr 15, 2014 15:15
por amigao » Ter Abr 15, 2014 15:15
- 4 Respostas
- 3997 Exibições
- Última mensagem por e8group

Dom Mai 11, 2014 17:09
Sequências
-
- Sequencia
por Amparo » Dom Mar 09, 2008 16:26
- 3 Respostas
- 3597 Exibições
- Última mensagem por nietzsche

Sex Set 02, 2011 00:42
Sequências
-
- Sequencia
por Abner » Qua Jan 26, 2011 19:15
- 1 Respostas
- 2410 Exibições
- Última mensagem por Neperiano

Qua Ago 31, 2011 18:43
Geometria Plana
-
- [Sequência]
por elizangelasss20 » Qua Abr 11, 2012 19:12
- 4 Respostas
- 2894 Exibições
- Última mensagem por elizangelasss20

Qua Abr 11, 2012 20:52
Sequências
-
- Sequência
por GrazielaSilva » Qui Nov 01, 2012 10:20
- 1 Respostas
- 3926 Exibições
- Última mensagem por young_jedi

Qui Nov 01, 2012 13:49
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  ,
, 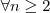 . Se
. Se  para
para  , prove que
, prove que 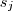 tem, no mínimo,
tem, no mínimo, 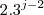 divisores positivos,
divisores positivos, 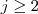 .
.

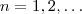 ,segue-se que
,segue-se que 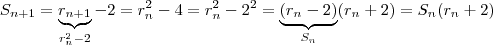 (Fórmula recursiva ) equivalentemente
(Fórmula recursiva ) equivalentemente 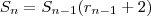 para
para 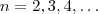 .
.  em função de
em função de  (a fórmula é válida sempre que o índice
(a fórmula é válida sempre que o índice 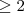 ) .Assim , por exemplo
) .Assim , por exemplo  . Em geral , tem-se
. Em geral , tem-se 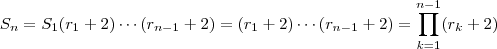 .
. , então
, então  .
.  (distintos) que é escrito como produto de
(distintos) que é escrito como produto de  termos distintos da lista
termos distintos da lista  para
para 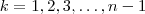 .A pergunta é , escolhendo-se
.A pergunta é , escolhendo-se  , quanto números
, quanto números 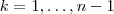 . Temos que a quantidade de k-uplas da forma
. Temos que a quantidade de k-uplas da forma 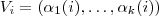 de modo que
de modo que ![[\alpha_1(i) \cdots \alpha_k(i) ] \neq [\alpha_1(j) \cdots \alpha_k(j) ] \forall i\neq j [\alpha_1(i) \cdots \alpha_k(i) ] \neq [\alpha_1(j) \cdots \alpha_k(j) ] \forall i\neq j](/latexrender/pictures/423edf12a4f723dc7d64384e7e303491.png) , com
, com  sendo algum dos
sendo algum dos  é
é  que é a mesma quantidade de produtos distintos da forma
que é a mesma quantidade de produtos distintos da forma 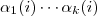 .
.  e
e  .
. 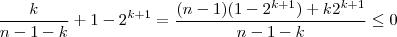
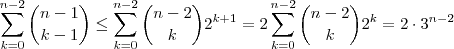 .
.
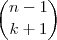 e não
e não  ...
... 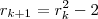 sempre que
sempre que 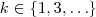 , então
, então 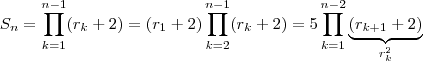 sempre que
sempre que 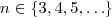 . Por este lado , nota-se que algum dos divisores de
. Por este lado , nota-se que algum dos divisores de  com
com 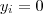 ou
ou  .
.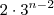 (se não errei contas ) ; logo este número sempre cumpre com o mínimo requerido .Mas vale ressaltar a importância de usar a indução matemática , essa sim é mais é mais precisa e formal . Pode-se que fizemos algumas afirmações que não cumprem com os termos depois dos "..." , pq não ?
(se não errei contas ) ; logo este número sempre cumpre com o mínimo requerido .Mas vale ressaltar a importância de usar a indução matemática , essa sim é mais é mais precisa e formal . Pode-se que fizemos algumas afirmações que não cumprem com os termos depois dos "..." , pq não ?

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.