Segue minha dicas .
Proposta 1 : Indução Matemática . Está familiarizado com indução ?
Proposta 2 . Para
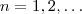
,segue-se que
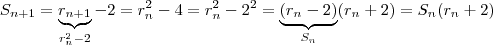
(Fórmula recursiva ) equivalentemente
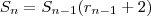
para
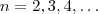
.
Podemos utilizar a fórmula recursiva para escrever

em função de

(a fórmula é válida sempre que o índice
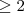
) .Assim , por exemplo

. Em geral , tem-se
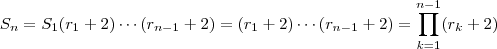
.
Deixe

, então

.
A ideia agora é encontrar todos números

(distintos) que é escrito como produto de

termos distintos da lista

para
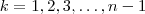
.A pergunta é , escolhendo-se

números acima dentro dos

, quanto números

teremos ?? A respota p/ está pergunta será a quantidade mínima [/tex] .
Para cada
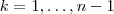
. Temos que a quantidade de k-uplas da forma
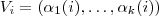
de modo que
![[\alpha_1(i) \cdots \alpha_k(i) ] \neq [\alpha_1(j) \cdots \alpha_k(j) ] \forall i\neq j [\alpha_1(i) \cdots \alpha_k(i) ] \neq [\alpha_1(j) \cdots \alpha_k(j) ] \forall i\neq j](/latexrender/pictures/423edf12a4f723dc7d64384e7e303491.png)
, com

sendo algum dos

é

que é a mesma quantidade de produtos distintos da forma
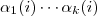
.
Logo , o n° mínimo requerido é

e

.
Desde que ,
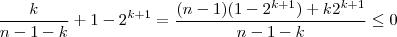
Segue-se que
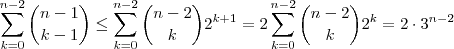
.
Aí fica minhas sugestões ; acho que a
proposta 1 é mais adequada .
 e
e  ,
, 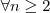 . Se
. Se  para
para  , prove que
, prove que 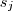 tem, no mínimo,
tem, no mínimo, 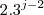 divisores positivos,
divisores positivos, 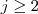 .
.

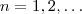 ,segue-se que
,segue-se que 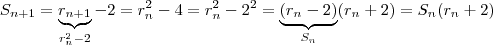 (Fórmula recursiva ) equivalentemente
(Fórmula recursiva ) equivalentemente 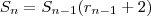 para
para  .
.  em função de
em função de  (a fórmula é válida sempre que o índice
(a fórmula é válida sempre que o índice 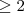 ) .Assim , por exemplo
) .Assim , por exemplo  . Em geral , tem-se
. Em geral , tem-se 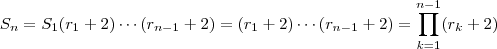 .
. , então
, então  .
.  (distintos) que é escrito como produto de
(distintos) que é escrito como produto de  termos distintos da lista
termos distintos da lista  para
para 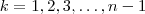 .A pergunta é , escolhendo-se
.A pergunta é , escolhendo-se  , quanto números
, quanto números 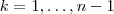 . Temos que a quantidade de k-uplas da forma
. Temos que a quantidade de k-uplas da forma 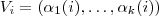 de modo que
de modo que ![[\alpha_1(i) \cdots \alpha_k(i) ] \neq [\alpha_1(j) \cdots \alpha_k(j) ] \forall i\neq j [\alpha_1(i) \cdots \alpha_k(i) ] \neq [\alpha_1(j) \cdots \alpha_k(j) ] \forall i\neq j](/latexrender/pictures/423edf12a4f723dc7d64384e7e303491.png) , com
, com  sendo algum dos
sendo algum dos  é
é  que é a mesma quantidade de produtos distintos da forma
que é a mesma quantidade de produtos distintos da forma 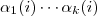 .
.  e
e  .
. 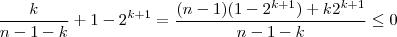
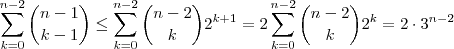 .
.
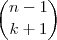 e não
e não  ...
... 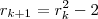 sempre que
sempre que 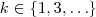 , então
, então 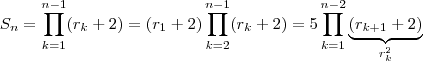 sempre que
sempre que 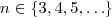 . Por este lado , nota-se que algum dos divisores de
. Por este lado , nota-se que algum dos divisores de  com
com 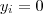 ou
ou  .
.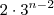 (se não errei contas ) ; logo este número sempre cumpre com o mínimo requerido .Mas vale ressaltar a importância de usar a indução matemática , essa sim é mais é mais precisa e formal . Pode-se que fizemos algumas afirmações que não cumprem com os termos depois dos "..." , pq não ?
(se não errei contas ) ; logo este número sempre cumpre com o mínimo requerido .Mas vale ressaltar a importância de usar a indução matemática , essa sim é mais é mais precisa e formal . Pode-se que fizemos algumas afirmações que não cumprem com os termos depois dos "..." , pq não ?