Neste exercício, tentei usar a fórmula
e 
em que:Tgx=Senx/Cosx
-3=Senx/Cosx
Senx=-3Cosx
Agora substituindo na fórmula 2:
![{Sen}^{2}x+{Cos}^{2}x=1
{3Cos}^{2}x+{Cos}^{2}x=1
{4Cos}^{2}x=1
{Cos}^{2}x=\frac{1}{4}
Cosx=\sqrt[2]{\frac{1}{4}}](/latexrender/pictures/05d93f19cfdc099ae9f01a8dd4ea352b.png "{Sen}^{2}x+{Cos}^{2}x=1
{3Cos}^{2}x+{Cos}^{2}x=1
{4Cos}^{2}x=1
{Cos}^{2}x=\frac{1}{4}
Cosx=\sqrt[2]{\frac{1}{4}}")
Porém, esse não é o resultado e não sei nenhum outro modo de realizar esse exercício, por isso preciso de ajuda e agradeço desde já pela atenção.
Obs.: GABARITO A
Bruno.
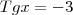
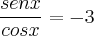
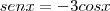
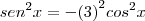(1)
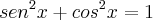
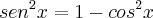(2)
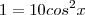
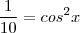
![cosx = + \sqrt[2]{10}/10](/latexrender/pictures/3f442bd74a45541bf90e00299b0cb690.png "cosx = + \sqrt[2]{10}/10")
ou ![cosx = - \sqrt[2]{10}/10](/latexrender/pictures/bdc09a6911118e46c95cdd6023de8928.png "cosx = - \sqrt[2]{10}/10")
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)