Olá, gostaria de tirar uma dúvida.
Se possuo uma sequência an, tal que an>0 para todo n>=0, e \Sigma an diverge, então mostre que \Sigma an/(an+1) também diverge.
Tentei separar a série em uma soma de duas outras séries, mas acabou não dando certo. Alguém poderia ajudar ??
Obrigada !!


 ou
ou  . Vamos considerar que estamos no segundo caso .
. Vamos considerar que estamos no segundo caso .  e
e  onde
onde  .
. 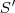 converge então
converge então  . Segue-se,
. Segue-se,  .
.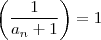 e assim
e assim  .
. diverge e
diverge e  , não podemos ter
, não podemos ter 
 é divergente então
é divergente então  que é menor que
que é menor que  e
e 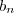 também é. Da mesma forma, se
também é. Da mesma forma, se  e
e  .
. , logo
, logo  diverge .
diverge . tal que
tal que  (a_n é limitado inferiormente por 0 e superiormente por M ) . Daí segue
(a_n é limitado inferiormente por 0 e superiormente por M ) . Daí segue  . Como
. Como  é uma constante , então a série
é uma constante , então a série  também diverge que por sua vez , a sua divergência implica a de
também diverge que por sua vez , a sua divergência implica a de ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)