 por leticia_08 » Sáb Abr 19, 2014 20:12
por leticia_08 » Sáb Abr 19, 2014 20:12
Olá, gostaria de tirar uma dúvida.
Se possuo uma sequência an, tal que an>0 para todo n>=0, e \Sigma an diverge, então mostre que \Sigma an/(an+1) também diverge.
Tentei separar a série em uma soma de duas outras séries, mas acabou não dando certo. Alguém poderia ajudar ??
Obrigada !!
-
leticia_08
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Abr 19, 2014 20:06
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Sáb Abr 19, 2014 22:19
por e8group » Sáb Abr 19, 2014 22:19
Boa noite leticia_08 . Por favor , sempre utilize o LaTeX . É difícil entender as expressões , não entendo se vc quer dizer

ou

. Vamos considerar que estamos no segundo caso .
Pensei em provar por contradição , o que acha ?
Denote

e

onde

.
Se
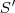
converge então

. Segue-se,

.
Logo
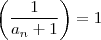
e assim

.
Desde que

diverge e

, não podemos ter

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Dom Abr 20, 2014 00:29
por Russman » Dom Abr 20, 2014 00:29
Se

é divergente então

que é menor que

tem de divergir também. Não? :|
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por e8group » Dom Abr 20, 2014 00:41
por e8group » Dom Abr 20, 2014 00:41
Sim a desigualdade é verdadeira . Mas como prova partindo dela ? Comparação direta ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Dom Abr 20, 2014 00:58
por Russman » Dom Abr 20, 2014 00:58
Eu pensei em comparação. Claro que se

e

é convergente, então
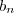
também é. Da mesma forma, se
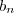
é divergente então

também. Mas sabemos que

é divergente. Não sei se na última afirmação vale a recíproca.
A comparação no limite, acho eu, é inconclusiva pq não quer dizer que o limite de

é não-nulo só pq

é divergente. Pode ser que sim, né.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por e8group » Dom Abr 20, 2014 11:49
por e8group » Dom Abr 20, 2014 11:49
Tem razão Russman , o limite é inconclusivo , fácil encontrar contra-exemplos .

e

.
Pensei em trabalhar com

ilimitado e limitado .
No primeiro caso

, logo

diverge .
No segundo caso , temos que existe

tal que

(a_n é limitado inferiormente por 0 e superiormente por M ) . Daí segue

. Como

é uma constante , então a série

também diverge que por sua vez , a sua divergência implica a de

.
O que acham ??
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Dom Abr 20, 2014 13:42
por Russman » Dom Abr 20, 2014 13:42
Acho que a demonstração está coerente, santhiago. De sorte que os termos são todos positivos. ;D
Bom artifício quebrar a comparação dessa forma.
Editado pela última vez por
Russman em Dom Abr 20, 2014 13:44, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Dom Abr 20, 2014 13:42
por Russman » Dom Abr 20, 2014 13:42
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Divergência] Dúvida em Divergência de campos vetoriais
por Lucasoaresf » Dom Set 14, 2014 16:26
- 0 Respostas
- 1167 Exibições
- Última mensagem por Lucasoaresf

Dom Set 14, 2014 16:26
Cálculo: Limites, Derivadas e Integrais
-
- [Séries] Sobre simplicação de expressões em séries
por HenriqueOrlan » Sáb Nov 21, 2015 11:28
- 1 Respostas
- 3727 Exibições
- Última mensagem por adauto martins

Qua Nov 25, 2015 16:31
Sequências
-
- [Séries] Série convergente ou divergente?
por RafaelPereira » Ter Jun 18, 2013 13:31
- 2 Respostas
- 2386 Exibições
- Última mensagem por RafaelPereira

Ter Jun 18, 2013 17:49
Sequências
-
- [Séries] Há uma fórmula explicita para esta série?
por Rilke » Sáb Out 13, 2012 13:42
- 5 Respostas
- 2538 Exibições
- Última mensagem por Rilke

Dom Out 14, 2012 16:50
Sequências
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3686 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ou
ou  . Vamos considerar que estamos no segundo caso .
. Vamos considerar que estamos no segundo caso .  e
e  onde
onde  .
. 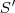 converge então
converge então  . Segue-se,
. Segue-se,  .
.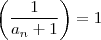 e assim
e assim  .
. diverge e
diverge e  , não podemos ter
, não podemos ter 
 é divergente então
é divergente então  que é menor que
que é menor que  e
e 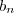 também é. Da mesma forma, se
também é. Da mesma forma, se  e
e  .
. , logo
, logo  diverge .
diverge . tal que
tal que  (a_n é limitado inferiormente por 0 e superiormente por M ) . Daí segue
(a_n é limitado inferiormente por 0 e superiormente por M ) . Daí segue  . Como
. Como  é uma constante , então a série
é uma constante , então a série  também diverge que por sua vez , a sua divergência implica a de
também diverge que por sua vez , a sua divergência implica a de 